Section 4

Differentiability and continuity

Generally, a function \(f(x)\) is differentiable at \(x_{0}\) if its graph has a unique tangent line at \((x_{0},f(x_{0}))\). To be differentiable at \(x_{0}\), the function must be continuous at \((x_{0},f(x_{0}))\). A function is continuous at \(x_{0}\) if its graph has no jump at \((x_{0},f(x_{0}))\). The following function in Figure 3 is not continuous at \(x_{0} = 0\), therefore is not differentiable at \(x_{0} = 0\)

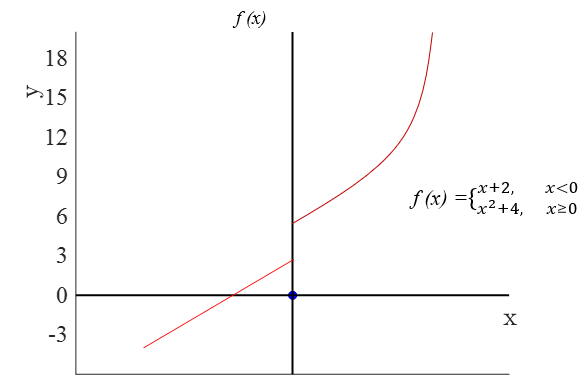
While continuity of the function at \((x_{0},f(x_{0}))\) is a necessary condition for the function to be differentiable at that point, it does not guarantee that the function is differentiable at that point. For example, while the function \(f(x) = 2 + \left | x \right |\) is continuous at \((0,2)\), it is not differentiable at \((0,2)\).

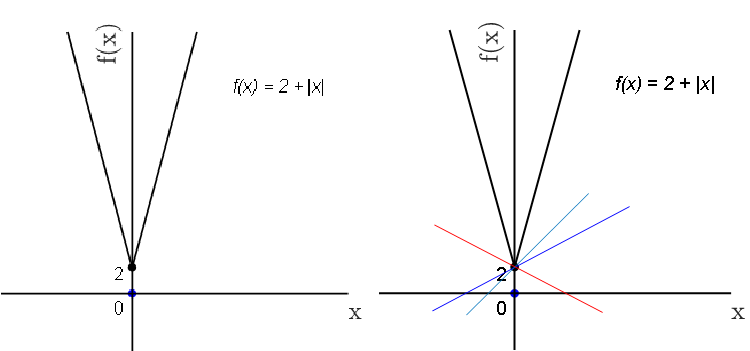
We draw the function \(f(x) = 2 + \left | x \right |\) in Figure 4(a) and 4(b). Figure 4(a) shows that the function is continuous at \((0,2)\). However, Figure 4(b) confirms that the function is not differentiable at the said point as there exists infinitely many lines at \((0,2)\) who are candidates to be the tangent line.