The Number Line, Cartesian Plane, and Sketching Graphs
Number line
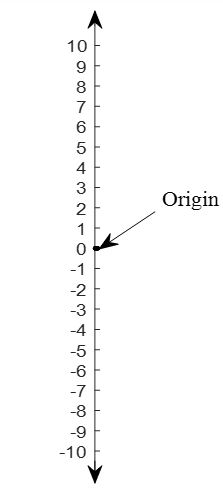
Number line: A number line is a line that contains all real numbers. The line extends to the right and left of the origin of the line up to the positive and negative infinity respectively. If the number line is a vertical line, it extends to the up and down of the origin of the line up to the positive and negative infinity respectively.
Origin: The number \(0\) is called the origin of the number line.
How we represent a number line which contains all real numbers? Using \(ℝ^1\). (Here, \(ℝ\) is a letter like character representing the number line).
Positive numbers along the number line: If the number line is a vertical line, then points to the upper side of the origin represent positive numbers. If the number line is a horizontal line, points to the right of the origin represent positive numbers.
Negative numbers along the number line: If the number line is a vertical line, then points __________ the origin represent negative numbers, and if the number line is a horizontal line, points to the __________ of the origin represent negative numbers.
below, left
Numbers in a number line
A number line contains all real numbers. In the number line, a basic unit of length is chosen, and successive intervals of this length measure the corresponding numbers. The further we move to the right from the origin, the bigger is the number. Negative numbers are represented by moving to the left of the origin.
Generally, a basic unit of length is chosen in each number line which measures one unit. Consecutive intervals of this length are marked. These marks are then numbered as \(+1, +2, +3,\) etc. on the right side (upper side) of the origin and as \(-1, -2, -3,\) etc. on the left side of the origin (below the origin).
However, to present big numbers in a number line, a basic unit of length can be chosen which itself includes some consecutive numbers. Suppose the absolute difference between the largest and the smallest number included in that basic length is, say \(k\). Successive intervals of the length from the origin are then marked as the \(n\)-multiple of the number \(k\), where in the right side of the origin \(n=1,2,3,\) etc. and in the left side of the origin \(n=-1,-2,-3,\) etc. For example, suppose on the number line a basic length is chosen each of which includes \(10\) successive numbers, i.e., the basic length measures 10 units. Now if we need to mark a number \(40\) in this number line, we need to mark the point in the right side of the origin with a distance from the origin which is \(4\) times of the basic length chosen. If we need to mark \(– 30\), we need to find the distance from the origin in the left side which is \(3\)-times of the basic length chosen.
Consider another example. Suppose, we need to mark \(1000\), and \(-1000\) in the number line. Although the number line contains all real numbers on both sides of the origin, we should not choose a basic length each of which measures one unit. If we choose a basic length each of which measures one unit, we will need to choose \(1000\) such marks to mark \(1000\), and it will be a mess. Better, choose a basic length which will measure a big unit, say \(100\), and in that case, we need to choose only \(10\) such markers on each side of the number line. By clicking the Right arrow button, see some examples of the number lines.
Some number lines


Test yourself 1: understanding the number line

See the number line \( ℝ^1\).
Which point represents the number \(900\)?
Which point represents the number \(- 600\)?
Point B represents the real number __________.
This number line only contains \(7\) real numbers: \(-900,-600,-300,0,300,600,900\). True or false?
[Click Right arrow button to see the answers.]
Answer: Test yourself 1

See the number line \( ℝ^1\) in Figure 4.
Which point represents the number \(900\)?
Answer: D
Which point represents the number \(- 600\)?
Answer: A
Point B represents the real number __________.
Answer: \(-900\)
This number line only contains \(7\) real numbers: \(-900,-600,-300,0,300,600,900\). True or false?
Answer: False. The number line contains all real numbers on the number line.
The coordinate system, Cartesian plane, Euclidian 2-space
It follows from the discussion in the previous slides is that any point on the number line \( ℝ^1\) corresponds to one and only one real number. The number line \( ℝ^1\) can be drawn as a horizontal line or as a vertical line.
Cartesian plane (also called Euclidean 2-space) or \( ℝ^2\)
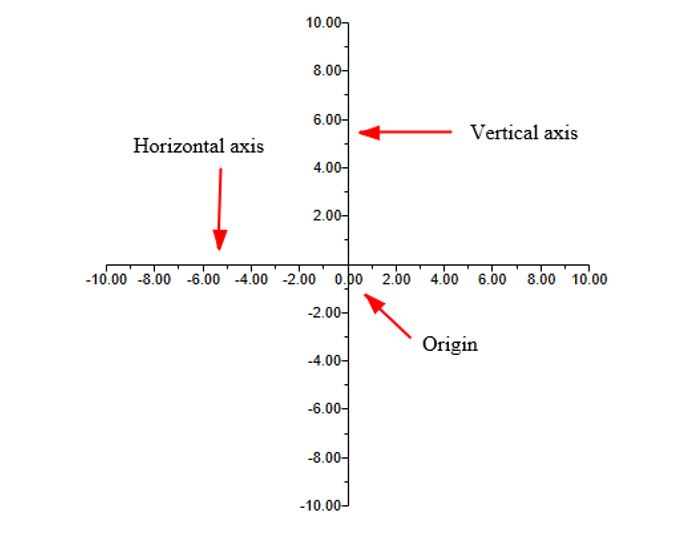
If we draw two perpendicular number lines, one a horizontal line and the other a vertical line, and they intersect at the origin \(0\); we get a coordinate system which is also called the Cartesian plane and is written as \( ℝ^2\). The Cartesian plane is also called the Euclidean 2-space. The two number lines in the Cartesian plane go off to infinity in the four directions from the origin: right, left, up and down, and contain ordered pairs of numbers \((x,y).\) On a Cartesian plane, the horizontal number line going through the origin is called the horizontal axis or the \(x\)-axis. The number line passes through the origin vertically is the vertical axis or the \(y\)-axis.
Click the Right arrow button and see a coordinate system or the Cartesian plane.
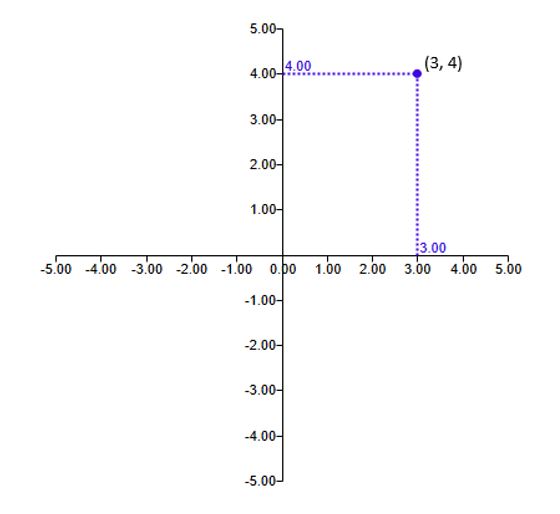
Ordered pair
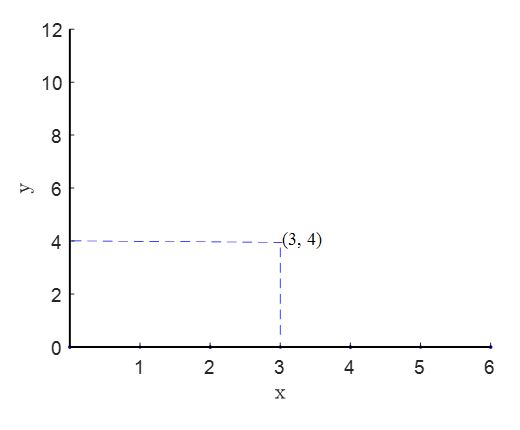
Any point in the Cartesian plane corresponds to an ordered pair of numbers \((x,y)\). Suppose one such point is \((3,4)\). This means vertically below this point the number line representing as the horizontal axis measures the real number \(3\) which is the \(x\)-value. On the other hand, the real number horizontally across from the point \((3,4)\) on the vertical axis represents the \(y\)-value \(4\). See Figure 6 showing the ordered pair of point \((3,4)\) in a Cartesian plane and the corresponding numbers on the horizontal and vertical number lines or the axes.
Test yourself 2: sketching ordered pairs
See Figure 6 again showing an ordered pair of point \((3,4)\) in a Cartesian plane and the corresponding numbers on the horizontal and vertical number lines or the axes.
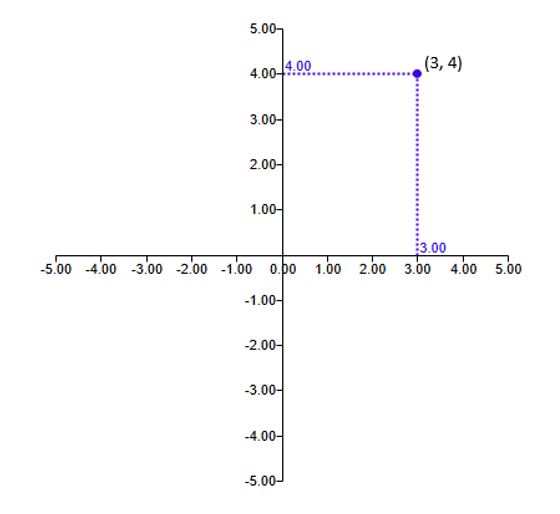
Now think about two more points \((-3,3)\) and \((2,-2)\). Where should you place these numbers?
Try to identify these two points by yourself before moving to the next slide.
Click the Right arrow button and see the Cartesian plane showing these three ordered pairs: \((3,4)\), \((-3, 3)\) and \((2, -2)\).
Answer: Test yourself 2

Test yourself 3: sketching ordered pairs
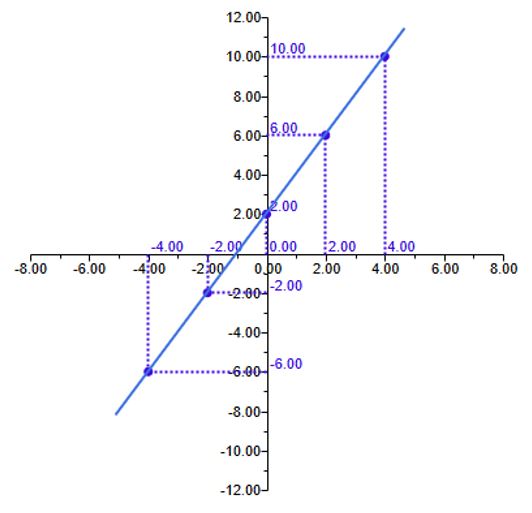
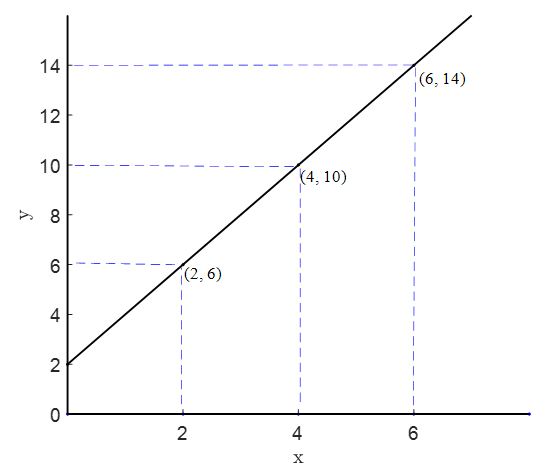
You are given a coordinate system below. (You know by this time that this is also called the Cartesian plane or the Euclidean 2-space. We will call it the Cartesian plane from now.) In a page draw this Cartesian plane and identify the following ordered pairs of \((x, y)\): \((-4,-6)\), \((-2, -2)\), \((0, 2)\), \((2,6)\) and \((4,10)\). Draw a straight line connecting these points. Please first try it by yourself before clicking the Right arrow button.
Click the Right arrow button to see the ordered pairs and the connecting line.
Answer: Test yourself 3
Test yourself 4: Sketching ordered pairs
See the Cartesian plane below.
You are given two relations to draw in the Cartesian plane.
$$y = 1 + 2x$$
$$y = 7 - x$$
Find the following ordered pairs:
| \(\;\; x \quad\) | \( \quad y = 1 + 2 x \quad\) | \( \quad y = 7 - x \quad\) |
| \(\;\; -2 \quad\) | ||
| \(\;\; 0 \quad\) | ||
| \(\;\; 2 \quad\) | ||
| \(\;\; 4 \quad\) |
Draw the Cartesian plane in a page. Draw these ordered pairs and connect the corresponding points in the Cartesian plane. Check answer in the next page clicking the Right arrow button.
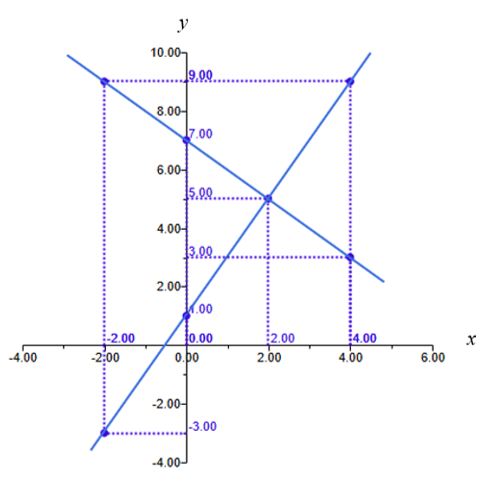
Answer: Test yourself 4
You are given two relations to draw in the Cartesian plane. $$y = 1 + 2x$$ $$y = 7 - x$$ The following ordered pairs correspond to the above relations. Figure 11 shows the ordered pairs in the Cartesian plane and the connecting lines correspond to the given relations.
| \(\;\; x \quad\) | \(\quad y = 1 + 2 x \quad\) | \(\quad y = 7 - x \quad\) |
| \(\;\; -2 \quad\) | \(-3\) | \(9\) |
| \(\;\; 0 \quad\) | \(1\) | \(7\) |
| \(\;\; 2 \quad\) | \(5\) | \(5\) |
| \(\;\; 4 \quad\) | \(9\) | \(3\) |
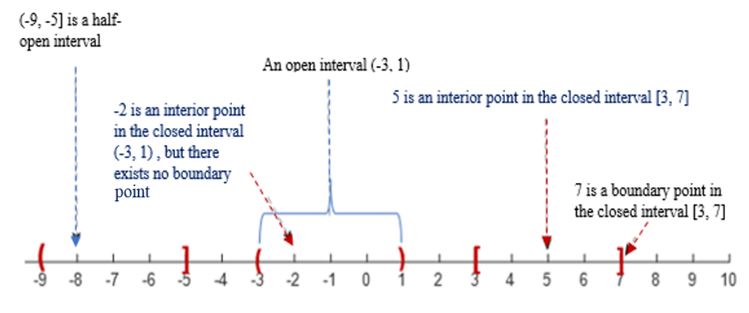
Intervals, interior points, boundary points
Another essential concept you frequently see in intermediate economics courses is the interval. A brief overview of some intervals is presented below.
Closed and open intervals
Consider a number line \( ℝ^1\). Suppose two points in this number line are \(m, n\) and suppose \(n>m\). Using \(m, n\) we can define the following intervals:
Closed interval: \([m,n] = \) {\(xϵ ℝ : m≤x≤n\)}
Open interval: \((m,n) = \) {\(xϵ ℝ : m<x<n\)}
Half-open intervals: \((m,n]\) and \([m,n)\)
An open interval contains all numbers between \(m\) and \(n\) but excludes \(m\) and \(n\) and is represented by the ‘Round’ brackets.
A closed interval contains all numbers between \(m\) and \(n\) including \(m\) and \(n\) and is represented by the ‘Squared’ brackets.
Interior point and boundary point:
Boundary point: if \(m\) is a boundary point of an interval \([m,n]\), every other interval containing \(m\) as an interior point must contain some points that are in \([m, n]\) and some points that are not in \([m, n]\).
Interior point: suppose \(c\) is an interior point in any interval, say \([m,n]\) (or \((m, n)\)). Then it is always possible to find an interval around the point \(c\), possibly very small, that lies entirely inside \([m,n]\) (or \((m, n)\)).
See some examples of intervals, boundary points and interior points in the next slide.
Functions
Given two number lines representing \(x\) and \(y\) respectively. If we get a rule which assigns each real number representing \(x\) to one and only one real number representing \(y\), we call the rule a function and write it as: \(y=f(x)\).
For example, if a rule assigns to any number \(x\) the number which is three units smaller, that is if \(x=10\), the corresponding \(y=10-3=7\), we call the rule a function and present it as: \(y=f(x)=x-3\).
In the Cartesian plane where the horizontal axis measures the \(x\)-value, and the vertical axis measures the \(y\)-value, we can find some ordered pairs correspond to the given function, and by connecting these ordered pairs, we can draw the corresponding graph of the function. ( We can draw the graphs using other techniques such as by finding the slope, vertical intercepts, optimal points, etc. which we discuss in other chapters.)
In a function \(y=f(x)\), the set of the values representing \(x\) is called the domain, and the set of values representing \(y\) is called the range or codomain. Variable \(x\) is the independent variable and is measured in the horizontal axis and \(y\) is the dependent variable which is measured in the vertical axis. [ To read more about the domain and variables, please see the resources on linear functions and graphs, and also read a recommended book (books)].
Test yourself 5: sketching the linear function using the ordered pairs
See the Cartesian plane which shows an ordered pair \((4,10)\) correspond to the function \(y=2x+2\). Redraw the Cartesian plane in a page. Now identify by yourself some ordered pairs correspond to the function \(y=2x+2\) and connect the points representing these ordered pairs. The connecting line should be a straight line and upward-sloping. See your answer by clicking the Right arrow button.
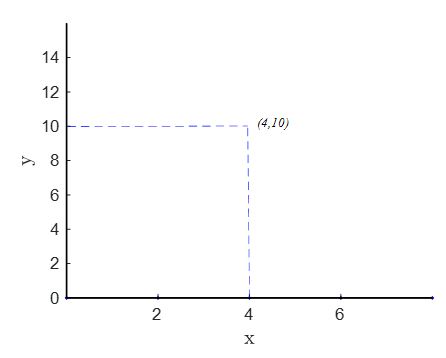
Answer: Test yourself 5
Test yourself 6: sketching the linear function using the ordered pairs
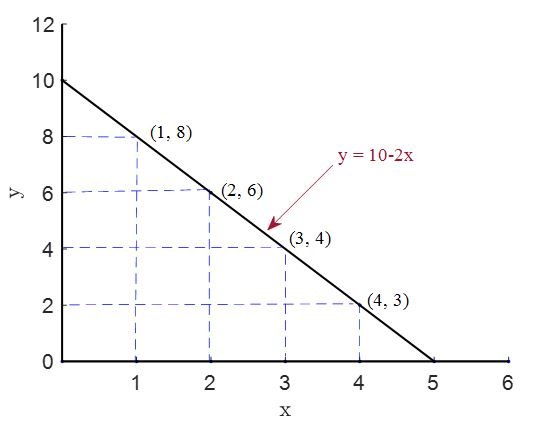
Redraw the following Cartesian plane in a page. Identify some ordered pairs correspond to the function \(y=10-2x\) and connect the points representing the ordered pairs. Is the line representing the function upward-sloping? Non-linear? See the answer by clicking the Right arrow button.
Answer: Test yourself 6
Test yourself 7: sketching the linear function using the ordered pairs
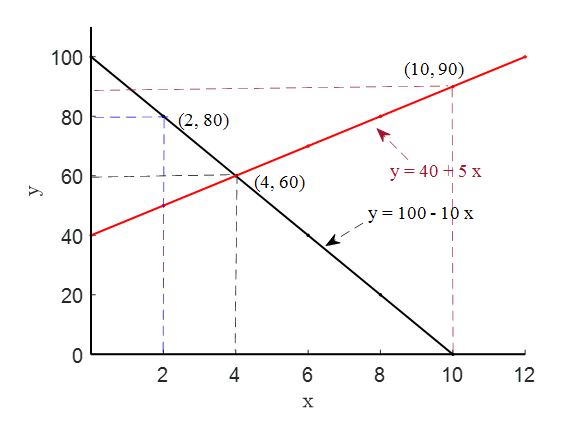
Draw the following functions by selecting some ordered pairs representing the functions. Do they cross in a point? Identify the ordered pair from the graph that is common in both functions. See by clicking the Right arrow button.
| \(y\) | \(=\) | \(100-10x\) |
| \(y\) | \(=\) | \(40+5x\) |

Answer: Test yourself 7
Test yourself 8: understanding the rules corresponding to the functions
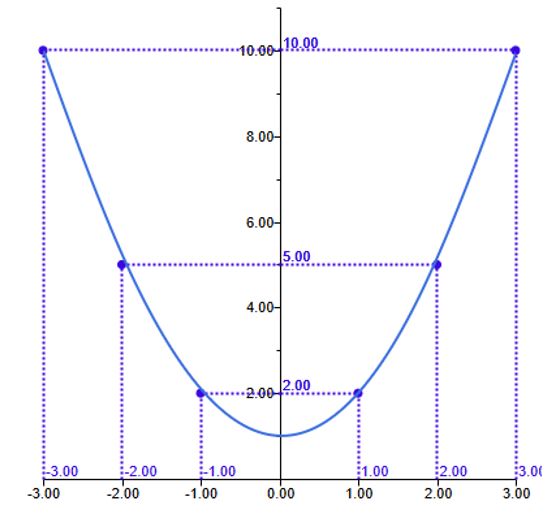
Suppose \(y=f(x)\). Suppose the rule assigns each number in \( ℝ^1\) representing \(x\), to the number which is one unit larger than the square of the ‘number representing \(x\)’. Write the function. $$y=f(x)=\text{__________}$$ For this function find the ordered pairs for the \(x\)-values \(-2\), \(-1\), \(0\), \(1\) and \(2\). Identify these ordered pairs in the Cartesian plane (or coordinates, or the Euclidean 2-space) and connect these points. Do you get a straight line? If not, don’t worry, functions can also be non-linear. Click the and verify your answer by clicking the Right arrow button.
Answer: Test yourself 8
Suppose \(y=f(x)\). Suppose the rule assigns each number is \( ℝ^1\) representing \(x\), to the number which is one unit larger than the square of the number representing \(x\). The function corresponding to this rule is: $$y=f(x)=1+x^2$$
Recommended Books
If you want to learn more about the Number lines, \( ℝ^1, ℝ^2, ℝ^n,\) Cartesian space, intervals, Euclidean space, functions, domains etc. you can read the following books:
Carl Simon, Lawrence Blume, Mathematics for Economists, W.W. Norton & Company.
Michael Hoy, John Livernois, Chris McKenna, Ray Rees, and Thanasis Stengos, Mathematics for Economics, PHI Learning Private Limited.
If you are enrolled for the e-book of Pearson, Canada, ‘Microeconomics: Canada in the Global Environment,’ you can use their ‘Grapher’ software to draw and understand the graphs. It is a cool software to understand how to choose ordered pairs and sketch the graphs.

UWO Economics Math Resources by Mohammed Iftekher Hossain is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.