Section 1
Solving two simultaneous equations and two unknowns
A solution of a pair of simultaneous equations is a pair of values for the unknowns which satisfies both equations in the system.
Not all sets of linear simultaneous equations have solutions. The necessary condition for the existence of a unique solution in a system of linear simultaneous equations is that the number of unknowns and the number of independent equations are equal. However, meeting this condition does not always guarantee the existence of a unique solution. (See Section 2)
If a unique solution exists for a system of linear simultaneous equations, it can be solved using several approaches. Most commonly used methods are the method of elimination, the method of substitution, and the graphical approach. In a system of linear simultaneous equations if a unique solution exists, the solution can also be derived using the matrix algebra, for example, by using the Cramer’s rule, or by using the matrix inversion, etc. When such a system has many unknowns and many variables, then software, such as Excel, can be used to find the solution.
These approaches to solving a system of linear simultaneous equations are not defined in this chapter. This chapter only shows how some of these approaches can be applied to get the solutions. A list of books is provided at the end of this chapter so that the readers can read more about the approaches to solve the system of linear simultaneous equations.
Example 1
Given the simultaneous equations
$$\; 2x + 3y = 11 \qquad\qquad(1)$$ $$-x + 2y = 12 \qquad\qquad(2)$$
Solve for \(x\) and \(y\) using the elimination approach.
Step 1: Multiply equation (2) by \(2\) $$-2x + 4y = 24 \qquad\qquad(3)$$
Step 2: Add equations \((1)\) and \((3)\) to eliminate \(x\) from the system of equations: $$\;\;\; 2x + 3y = 11$$ $$\frac{\qquad -2x + 4y = 24\qquad}{\quad\; 0 + 7y = 35}$$
Step 3: Solve for \(y\) $$y = \frac{35}{7} = 5$$
Step 4: Solve for \(x\) by substituting \(y = 5\) into any of the equations $$\;\;\; 2x + 3y = 11$$ $$2x + 3(5) = 11$$ $$\qquad\qquad\qquad\qquad 2x = 11 - 15 = -4$$ $$\qquad\qquad x = -2$$
Example 2
Given the simultaneous equations
$$\;\;\; 6x - y = 4 \qquad\qquad(1)$$ $$-x + 4y = 7 \qquad\qquad(2)$$
Solve for \(x\) and \(y\) using the substitution approach.
From equation (1) find the expression for \(y\) in terms of \(x\): $$6x - 4 = y$$ $$\qquad\qquad\;\; y = 6x - 4$$ Substitute \(y=6x-4\) for \(y\) in equation (2): $$\qquad\quad -x + 4y = 7$$ $$-x + 4(6x - 4) = 7$$ $$\; -x + 24x - 16 = 7$$ $$\qquad\qquad\quad\;\;\, 23x = 23$$ $$\qquad\qquad\qquad\;\, x = 1$$ Substitute \(x=1\) into any of the equations to solve for \(y\) and get: $$y = 2$$
Example 3
Given the linear simultaneous equations $$60 - 4y - 12x = 0 \qquad\qquad(1)$$ $$\;\; 34 - 6y - 4x = 0 \qquad\qquad(2)$$
Solve for \(x\) and \(y\) graphically.
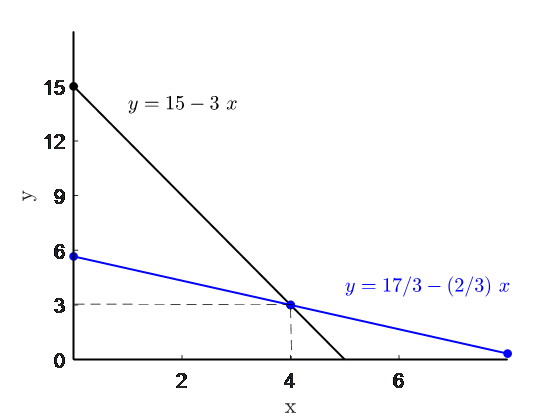
Rewrite the equations (1) and (2) as: $$y = 15 - 3x$$ $$\quad y = \frac{17}{3} - \frac{2}{3}x$$
The two lines are plotted in Figure 1.
The point of intersection is the solution. The lines intersect only at one point \((4,3)\). In this case \((4,3)\) is the unique solution.
Figure 1 Unique solution

UWO Economics Math Resources by Mohammed Iftekher Hossain is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.