Test Yourself and Learn: Matrix Algebra
Question 1. (Dimensions and elements of a matrix)
Given the matrix
$$A=\begin{bmatrix}6&8&2&3\\7&5&4&2\\0&1&9&4\end{bmatrix}$$
a) Write the dimensions of the matrix. How to read the dimensions?
b) Which element is \(a_{23}\)?
c) Which element is \(a_{32}\)?
Q1 Answer
Given the matrix
$$A=\begin{bmatrix}6&8&2&3\\7&5&\color{red}{4}&2\\0&\color{red}{1}&9&4\end{bmatrix}$$
a) The dimensions of the given matrix are \(3\)×\(4\). This matrix has \(3\) rows and \(4\) columns which define its dimensions. The dimensions \(3\)×\(4\) are read as “\(3\) by \(4\)”.
b) The element \(a_{23}\) in a matrix is the element which is in its second row and third column. In this example, \(a_{23}=\color{red}{4}\).
c) The element \(a_{32}\) is \(\color{red}{1}\).
Note:
A matrix contains numbers, parameters, or variables in a rectangular (or rounded) array, in an ordered location for each element.
Dimensions of a matrix show the number of rows \((r)\) and columns \((c)\) in the matrix and is written as (\(r×c\)), which is read as “\(r\) by \(n\)”.
If a matrix has \(2\) rows and \(3\) columns, its dimensions are (\(2\)×\(3\)). To indicate the dimensions of a matrix, the row number goes before the column number. So, if a matrix has \(2\) rows and \(3\) columns, it’s dimensions cannot be written as (\(3\)×\(2\)).
If a matrix has only one row, its dimensions are (\(1\)×\(c\)) and it is called a row vector. If a matrix has only one column, its dimensions are (\(r\)×\(1\)) and it is a column vector.
Generally, we specify the location (or position) of an element in a matrix using the term \(a_{\color{red}{ij}}\). The element \(a_{ij}\) appears in the row \(i\) and column \(j\) of the matrix. For example, in the given matrix \(A\), the element \(a_{33}\) is \(9\) as it appears in the third row and third column. Show Question
Question 2.(Types of matrices)
Given
\(A=\begin{bmatrix}2&3&0\\4&3&7\end{bmatrix}\)
\(B=\begin{bmatrix}4&2\\2&3\end{bmatrix}\)
\(C=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\)
\(D=\begin{bmatrix}10&2&7\end{bmatrix}\)
\(E=\begin{bmatrix}12\\18\\23\end{bmatrix}\)
a) Which matrices are the square matrices?
b) Which one is an identity matrix?
c) Which one is a column vector?
d) Write the transpose matrix of \(A\).
Q2 Answer
Given
\(A=\begin{bmatrix}2&3&0\\4&3&7\end{bmatrix}\)
\(B=\begin{bmatrix}4&2\\2&3\end{bmatrix}\)
\(C=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\)
\(D=\begin{bmatrix}10&2&7\end{bmatrix}\)
\(E=\begin{bmatrix}12\\18\\23\end{bmatrix}\)
a) Matrix \(B\) and matrix \(C\) are the square matrices.
b) \(C\) is an identity matrix.
c) \(E\) is a column vector.
d) The transpose of \(A\) is.
$$A'=\begin{bmatrix}2&4\\3&3\\0&7\end{bmatrix}$$
Note:
In a square matrix, the number of rows and the number of columns are equal. For example, a matrix with dimensions (\(3\)×\(3\)) is a square matrix, but with dimensions (\(2\)×\(3\)) is not a square matrix.
An identity matrix is a square matrix in which every element on the principal diagonal has the value \(1\) and all other elements are \(0\). The identity matrix is generally denoted by \(\color{red}{I}\). Any matrix \(A\) multiplied by the identity matrix \(I\) (or, vice versa), if multiplication is possible, is the given matrix \(A\).
Given a matrix \(A\). If we convert the rows of \(A\) to columns or vice versa, we get the transpose matrix of \(A\), which is written as \(A'\).
A null matrix is a matrix where all elements are \(0\).Show Question
Question 3.(Uses of the matrix)
A firm with \(3\) retail stores has \(15\) TVs \((t)\), \(10\) computers \((c)\) and \(12\) recorders \((r)\) in store \(1\); \(10\) TVs \((t)\), \(13\) computers \((c)\) and \(20\) recorders \((r)\) in store \(2\); and \(25\) TVs \((t)\), \(15\) computers \((c)\) and \(5\) recorders \((r)\) in store \(3\). In matrix form express the present inventory.
Q3 Answer
A firm with \(3\) retail stores has \(15\) TVs \((t)\), \(10\) computers \((c)\) and \(12\) recorders \((r)\) in store \(1\); \(10\) TVs \((t)\), \(13\) computers \((c)\) and \(20\) recorders \((r)\) in store \(2\); and \(25\) TVs \((t)\), \(15\) computers \((c)\) and \(5\) recorders \((r)\) in store \(3\). In matrix form, its present inventory is:
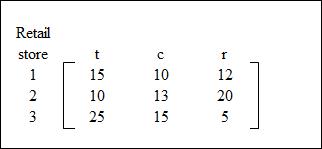
Note
Matrix algebra permits expression of information in a simplified way.
In real life, we use matrices in several ways, even though all of we are not aware of the matrices around us and its properties in detail.
In economics and business matrices play important roles, for example (i) to present a system of linear equations (and non-linear equations after performing linear transformation) in a simplified way, (ii) to determine the existence of solution (equilibrium values) in the system, and (iii) to solve the system if a solution exists. Show Question
Question 4. (Addition and subtraction)
Given four matrices
\(A=\begin{bmatrix}2&3&0\\4&3&7\end{bmatrix}\)
\(B=\begin{bmatrix}5&7\\6&4\end{bmatrix}\)
\(C=\begin{bmatrix}5&1\\2&3\end{bmatrix}\)
\(D=\begin{bmatrix}3&0\\2&1\end{bmatrix}\)
Find (i) \(A+B\), (ii) \(C+D\), and (iii) \(B – D\)
Q4 Answer
Given four matrices
\(A=\begin{bmatrix}2&3&0\\4&3&7\end{bmatrix}\)
\(B=\begin{bmatrix}5&7\\6&4\end{bmatrix}\)
\(C=\begin{bmatrix}5&1\\2&3\end{bmatrix}\)
\(D=\begin{bmatrix}3&0\\2&1\end{bmatrix}\)
(i) Matrices \(A\) and \(B\) are not conformable for addition as they have different dimensions.
(ii) Matrices \(C\) and \(D\) are conformable for addition as they have the same dimensions (\(2\)×\(2\))
$$C+D=\begin{bmatrix}5&1\\2&3\end{bmatrix}+\begin{bmatrix}\color{red}{3}&\color{red}{0}\\\color{red}{2}&\color{red}{1}\end{bmatrix}=\begin{bmatrix}5+\color{red}{3}&1+\color{red}{0}\\2+\color{red}{2}&3+\color{red}{1}\end{bmatrix}=\begin{bmatrix}8&1\\4&4\end{bmatrix}$$
(iii) Matrices \(B\) and \(D\) are conformable for subtraction as they have the same dimensions (\(2\)×\(2\))
$$B-D=\begin{bmatrix}5&7\\6&4\end{bmatrix}-\begin{bmatrix}\color{red}{3}&\color{red}{0}\\\color{red}{2}&\color{red}{1}\end{bmatrix}=\begin{bmatrix}5-\color{red}{3}&7-\color{red}{0}\\6-\color{red}{2}&4-\color{red}{1}\end{bmatrix}=\begin{bmatrix}2&7\\4&3\end{bmatrix}$$
Note:
Addition and subtraction of two matrices are only possible if two matrices are conformable for addition and subtraction. Two matrices of the same size (dimensions) are conformable for addition and subtraction. Addition of two matrices requires that each element of a matrix is added with the corresponding element of the other matrix. Subtraction of two matrices requires each element of one matrix to be subtracted from the corresponding element of the other matrix.
Show Question
Question 5. (Scalar multiplication)
Given
$$A=\begin{bmatrix}4&2&1\\3&1&0\\5&3&7\end{bmatrix}$$
Find \(kA\) where \(k\) is a scalar and \(k = 4\).
Q5 Answer
Given
$$A=\begin{bmatrix}4&2&1\\3&1&0\\5&3&7\end{bmatrix}$$
And \(k\) is a scalar where \(k = \color{red}{4}\).
$$kA=\color{red}{4}\begin{bmatrix}4&2&1\\3&1&0\\5&3&7\end{bmatrix}=\begin{bmatrix}4×\color{red}{{4}}&2×\color{red}{{4}}&1×\color{red}{{4}}\\3×\color{red}{{4}}&1×\color{red}{{4}}&0×\color{red}{{4}}\\5×\color{red}{{4}}&3×\color{red}{{4}}&7×\color{red}{{4}}\end{bmatrix}= \begin{bmatrix}16&8&4\\12&4&0\\20&12&28\end{bmatrix}$$
Note:
When a matrix is multiplied by an ordinary number (which is called a scalar in matrix algebra), that number must multiply every element of the matrix.
Show Question
Question 6. (Conformability for multiplication)
Given
\(A=\begin{bmatrix}2&3&0\\4&3&7\end{bmatrix}\)
\(B=\begin{bmatrix}5&7\\6&4\end{bmatrix}\)
\(C=\begin{bmatrix}5&1\\2&3\end{bmatrix}\)
Determine for each of the followings whether they are conformable for multiplication. If conformable for multiplication, indicate the dimensions of the product matrix.
$$AB BA BC CB$$
Q6 Answer
Given
\(A=\begin{bmatrix}2&3&0\\4&3&7\end{bmatrix}\)
\(B=\begin{bmatrix}5&7\\6&4\end{bmatrix}\)
\(C=\begin{bmatrix}5&1\\2&3\end{bmatrix}\)
\(AB\): If \(A\) is the lead matrix and \(B\) is the lag matrix, they are not conformable for multiplication as the number of columns in the lead matrix and the number of rows in the lag matrix are not equal: \(\color{red}{3≠2}\)
\(BA\): If \(B\) is the lead matrix and \(A\) is the lag matrix, they are conformable for multiplication as the number of columns in the lead matrix \(B\) and the number of rows in the lag matrix \(A\) are equal: \(\color{red}{2=2}\). And the dimensions of the product matrix is defined by the number of rows in the lead matrix \(B\) and the number of columns in the lag matrix \(A\), which are \(\color{red}{(2×3)}\).
\(BC\): Conformable for multiplication and the dimensions of the product matrix are \((2×2)\).
\(CB\): Conformable for multiplication and the dimensions of the product matrix are \((2×2)\).
Note:
Not all pairs of matrices are conformable for multiplication. Suppose a matrix \(A\) has dimensions \((\color{red}{m}×\color{blue}{n})\) and another matrix \(B\) has dimensions \((\color{blue}{r}×\color{red}{s})\) . The multiplication \(AB\) can only be performed if \((\color{blue}{n=r})\) , that is, if the number of columns in the first matrix (which is called the lead matrix) equals the number of rows in the second matrix (lag matrix). If \((\color{blue}{n=r})\) , then \(A\) and \(B\) are conformable for multiplication.
It is also important to consider the order in which matrices are multiplied. If \(A\) and \(B\) are conformable for multiplication, that does not automatically imply that \(B\) and \(A\) are also conformable for multiplication.
If multiplication is possible, the resulting matrix \(AB\) will have dimensions \((\color{red}{m}×\color{red}{s})\), that is, the number of rows is the lead matrix is the number of rows in the product matrix and the number of columns in the lag matrix is the number of columns in the product matrix.
See the following examples:
| Dimensions of matrix \(A\) | Dimensions of Matrix \(B\) | Dimensions of the product matrix \(AB\) |
| \(5×3\) | \(3×3\) | \(5×3\) |
| \(3×3\) | \(5×3\) | Not conformable for multiplication |
| \(1×4\) | \(4×1\) | \(1×1\) |
| \(1×4\) | \(1×4\) | Not conformable for multiplication |
| \(3×3\) | \(3×3\) | \(3×3\) |
Show Question
Question 7. (Matrix multiplication)
Given
$$A=\begin{bmatrix}2&3&0\\4&3&7\end{bmatrix} B=\begin{bmatrix}5&7\\6&4\end{bmatrix}$$
Find \(AB\) and \(BA\).
Q7 Answer
Given
$$A=\begin{bmatrix}2&3&0\\4&3&7\end{bmatrix} B=\begin{bmatrix}5&7\\6&4\end{bmatrix}$$
\(AB\): If \(A\) is the lead matrix and \(B\) is the lag matrix, they are not conformable for multiplication as the number of columns in \(A\) is not equal to the number of rows in \(B\), that is, \(3≠2\).
\(BA\): If \(B\) is the lead matrix and \(A\) is the lag matrix, they are conformable for multiplication and the dimensions of the product matrix \(BA\) is \(2×3\):
\(C=BA=\begin{bmatrix}5&7\\6&4\end{bmatrix}\begin{bmatrix}2&3&0\\4&3&7\end{bmatrix}\)
\(=\begin{bmatrix}r_1c_1&r_1c_2&r_1c_3\\r_2c_1&r_2c_2&r_2c_3\end{bmatrix}\)
\(=\begin{bmatrix}5(2)+7(4)&5(3)+7(3)&5(0)+7(7)\\6(2)+4(4)&6(3)+4(3)&6(0)+4(7)\end{bmatrix}\)
\(=\begin{bmatrix}38&36&49\\28&30&28\end{bmatrix}\)
Note
When \(2\) matrices are conformable for multiplication, to find an element of the product matrix \(C\), say \(\color{red}{c_{ij}}\)
- use only row \(i\) from the lead matrix and only column \(j\) from the lag matrix
- Multiply the row \(i\) of the lead matrix and column \(j\) of the lag matrix
- Multiplying the row \(i\) of the lead matrix and column \(j\) of the lag matrix requires to multiply each element of the row \(i\) of the lead matrix and the corresponding element of the column \(j\) of the lag matrix, followed by adding their products.
- In this example, to find the element \(\color{red}{c_{23}}\) in the product matrix, use only the second row of the lead matrix and the third column of the lag matrix, multiply the corresponding elements , and add their products:
\(C=BA=\begin{bmatrix}5&7\\\color{red}{6}&\color{red}{4}\end{bmatrix}\begin{bmatrix}2&3&\color{red}{0}\\4&3&\color{red}{7}\end{bmatrix}\)
\(=\begin{bmatrix}r_1c_1&r_1c_2&r_1c_3\\r_2c_1&r_2c_2&\color{red}{r_2c_3}\end{bmatrix}\)
\(=\begin{bmatrix}r_1c_1&r_1c_2&r_1c_3\\r_2c_1&r_2c_2&\color{red}{6(0)+4(7)}\end{bmatrix}\)
\(=\begin{bmatrix}r_1c_1&r_1c_2&r_1c_3\\r_2c_1&r_2c_2&\color{red}{28}\end{bmatrix}\)
Show Question
Question 8. (Matrix multiplication)
Given
$$C=\begin{bmatrix}5&1\\2&3\end{bmatrix} D=\begin{bmatrix}1&0\\0&1\end{bmatrix}$$
$$E=\begin{bmatrix}10&2&7\end{bmatrix} F=\begin{bmatrix}2\\1\\4\end{bmatrix}$$
Find \(CD\), \(DC\), and \(EF\).
Q8 Answer
Given
$$C=\begin{bmatrix}5&1\\2&3\end{bmatrix} D=\begin{bmatrix}1&0\\0&1\end{bmatrix}$$
$$E=\begin{bmatrix}10&2&7\end{bmatrix} F=\begin{bmatrix}2\\1\\4\end{bmatrix}$$
\(CD\): Conformable for multiplication. \(D\) is an identity matrix. Therefore, \(CD = C\)
$$CD=\begin{bmatrix}5&1\\2&3\end{bmatrix}\begin{bmatrix}1&0\\0&1\end{bmatrix}=\begin{bmatrix}5&1\\2&3\end{bmatrix}$$
\(DC\): Conformable for multiplication. \(D\) is an identity matrix. So, \(DC = C\).
\(EF\): If \(E\) is the lead matrix and \(F\) is the lag matrix, they are conformable for multiplication as the dimensions of the lead matrix are \((1×3)\) and the dimensions of the lag matrix are \((3×1)\).
Dimensions of their product matrix are \((1×1)\)
\(EF=\begin{bmatrix}10&2&7\end{bmatrix}\begin{bmatrix}\color{red}{2}\\\color{red}{1}\\\color{red}{4}\end{bmatrix}\)
\(=\begin{bmatrix}10(\color{red}{2})&2(\color{red}{1})&7(\color{red}{4})\end{bmatrix} =\begin{bmatrix}50\end{bmatrix}\)
Note:
If \(F\) is the lead matrix and \(E\) is the lag matrix, then also they are conformable for multiplication. The dimensions of the product matrix \(FE\) are not \((1×1)\) like the product matrix \(EF\). The dimensions of \(FE\) are \((3×3)\). Check, why?
The steps of matrix multiplication are:
► Check which one is the lead matrix, and which one is the lag matrix
► Check whether the given matrices are conformable for multiplication. Conformability requires that the number of columns in the lead matrix equals the number of rows in the lag matrix.
► If two matrices are conformable for multiplication, the dimensions of the product matrix are determined by the number of rows of the lead matrix and the number of columns of the lag matrix.
► When deriving an element of the product matrix, use the corresponding row form the lead matrix and the corresponding column from the lag matrix. Then, multiply the corresponding elements and add their products.
► Do lots of practice.
Show Question
Question 9. (Expressing a system of linear equations in matrix form)
Express the following system of linear equations in matrix form
$$4x+3y=14\\2x+5y=21$$
Q9 Answer
Given the system of linear equations
$$4x+3y=14\\2x+5y=21$$
Its matrix form is:
$$AX=B\\\begin{bmatrix}4&3\\2&5\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}14\\21\end{bmatrix}$$
Note:
A system of linear equations can be presented in matrix form. To present the system in matrix form
► use the coefficients in the system to form the coefficient matrix \(A\)
► form the column vector \(X\) using the variables.
► From the column vector \(B\) using the constants.
► Remember that when placing the coefficients, variables, and constants in the corresponding matrices, following the order is important.
Then write the system of linear equations as:
$$AX=B$$
Show Question
Question 10. (Expressing a system of linear equations in matrix form)
Write the following system of linear equations in matrix form
$$2x+4y-3z=24\\6x-10y+4z=52\\-2x+6y+4z=68$$
Q10 Answer
Given the system of linear equations
$$2x+4y-3z=24\\6x-10y+4z=52\\-2x+6y+4z=68$$
Its matrix form is:
$$AX=B\\\begin{bmatrix}2&4&-3\\6&-10&4\\-2&6&4\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}24\\52\\68\end{bmatrix}$$
Note:
If you change the positions of the variables in the column vector \(X\), you need to change the positions of the coefficients in the coefficient matrix accordingly. For example, the given system can also be expressed as:
$$AX=B\\\begin{bmatrix}2&\color{red}{-3}&\color{green}{4}\\6&\color{red}{4}&\color{green}{-10}\\-2&\color{red}{4}&\color{green}{6}\end{bmatrix}\begin{bmatrix}x\\\color{red}{z}\\\color{green}{y}\end{bmatrix}=\begin{bmatrix}24\\52\\68\end{bmatrix}$$
Show Question
Question 11. (Matrix form of a system of linear equations)
A system of linear equations is presented below in matrix from. Write the corresponding equation system.
$$AX=B\\\begin{bmatrix}2&1\\4&-3\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}15\\10\end{bmatrix}$$
Q11 Answer
Given the system of linear equations in matrix form
$$AX=B\\\begin{bmatrix}2&1\\4&-3\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}15\\10\end{bmatrix}$$
The corresponding system of linear equations is
$$2x+y=15\\4x-3y=10$$
Note:
• Generally, the first row in the coefficient matrix corresponds to the coefficients in the first equation, the second row corresponds to the second equation, and so on.
• The element in the first row in \(B\) corresponds to the constant in the first equation and in the second row corresponds to the constant in the second equation.
• Remember that the system consists of linear equations. Therefore, each term contains at most one variable, and if a term contains a variable, its exponent is \(1\).
Show Question
Question 12. (Matrix form to a system of equations)
A system of linear equations is presented below in matrix from. Write the corresponding equation system.
$$AX=B\\\begin{bmatrix}1&4&-3\\6&-10&4\\-2&6&0\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}24\\52\\40\end{bmatrix}$$
Q12 Answer
Given the system in matrix form
$$AX=B\\\begin{bmatrix}1&4&-3\\6&-10&4\\-2&6&0\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}24\\52\\40\end{bmatrix}$$
The corresponding equation system is
$$x +4y-3z =24\\6x-10y+4z=52\\-2x+6y=40$$
Question 13. (Determinants)
Given
$$A=\begin{bmatrix}2&3&0\\4&3&7\end{bmatrix} B=\begin{bmatrix}5&3\\2&4\end{bmatrix}$$
Find the determinants \(|A|\) and \(|B|\).
Q13 Answer
Given
$$A=\begin{bmatrix}2&3&0\\4&3&7\end{bmatrix} B=\begin{bmatrix}5&3\\2&4\end{bmatrix}$$
The determinant \(|A|\) cannot be determined as the matrix \(A\) is not a square matrix.
The determinant \(|B|\)is
$$|B|=\begin{vmatrix}5&3\\2&4\end{vmatrix}=5(4)-3(2)=14$$
Note:
Given a \(2×2\) matrix
$$A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}$$
The determinant is
$$|A|=\begin{vmatrix}\color{red}{a_{11}}&a_{12}\\a_{21}&\color{red}{a_{22}}\end{vmatrix}=\color{red}{a_{11} a_{22}}-a_{12} a_{21}$$
The steps are:
• Derive the product of the elements on the principal diagonal: \(\color{red}{a_{11} a_{22}}\)
• Derive the product of the elements off the principal diagonal: \(a_{12} a_{21}\)
• Take their difference:\(\color{red}{a_{11} a_{22}}-a_{12} a_{21}\)
Some key points regarding the determinants:
• The determinant of a square matrix can be calculated.
• If the determinant can be calculated, we get an ordinary number.
• If the determinant of a matrix is zero, the matrix is called a singular matrix. If a matrix is a singular matrix, there exists linear dependence between more than one column or row. If the determinant of a coefficient matrix is zero, \(\color{red}{|A|=0}\), the corresponding matrix is a singular matrix and a unique solution of the system does not exist.
• If in a system of linear equations, the determinant of the coefficient matrix is nonzero, \(\color{red}{|A|≠0}\), a unique solution in the system does exist, and the coefficient matrix is a nonsingular matrix.
Show Question
Question 14. (Determinants)
Given
$$A=\begin{bmatrix}4&2\\2&1\end{bmatrix} B=\begin{bmatrix}5&3\\3&4\end{bmatrix}$$
Which matrix is a singular matrix, and which one is a nonsingular matrix?
Q14 Answer
Given
$$A=\begin{bmatrix}4&2\\2&1\end{bmatrix} B=\begin{bmatrix}5&3\\3&4\end{bmatrix}$$
The determinant of matrix \(A\) is
$$|A|=\begin{vmatrix}4&2\\2&1\end{vmatrix}=4(1)-2(2)=4-4=0$$
Matrix \(A\) is a singular matrix.
The determinant of matrix \(B\) is
$$|B|=\begin{vmatrix}5&3\\3&4\end{vmatrix}=5(4)-3(3)=20-9=11$$
Matrix B is a nonsingular matrix.
Show Question
Question 15. (Determinants)
Given the system of linear equations
$$8x+4y=14\\4x+2y=21$$
Using the determinant of the coefficient matrix, check whether the system has a unique solution.
Q15 Answer
Given the system of linear equations
$$8x+4y=14\\4x+2y=21$$
The coefficient matrix is
$$A=\begin{bmatrix}8&4\\4&2\end{bmatrix}$$
The determinant of matrix \(A\) is
$$|A|=\begin{vmatrix}8&4\\4&2\end{vmatrix}=8(2)-4(4)=16-16=0$$
The coefficient matrix is a singular matrix. \(A\) unique solution does not exist for the given system of linear equations.
Note:
If the coefficient matrix is a singular matrix, it confirms that there exists linear dependence between at least two columns or two rows (and vice versa). This, in turn, confirms that in the equation system a unique solution does not exist.
Show Question
Question 16. (Determinants)
Given the system of linear equations
$$x+y=12\\2x-y=3$$
Using the determinant of the coefficient matrix, check whether the system has a unique solution.
Q16 Answer
Given the system of linear equations
$$x+y=12\\2x-y=3$$
The coefficient matrix is
$$A=\begin{bmatrix}1&1\\2&-1\end{bmatrix}$$
The determinant of matrix \(A\) is
$$|A|=\begin{vmatrix}1&1\\2&-1\end{vmatrix}=1(-1)-1(2)=-1-2=-3≠0$$
The coefficient matrix is a nonsingular matrix, and a unique solution does exist for the given system of linear equations.
Note:
If the coefficient matrix is a nonsingular matrix, it confirms that there exists no linear dependence between the columns and rows (and vice versa). As the coefficient matrix is a square matrix (number of unknowns in the system equals the number of equations), and non-singular (all equations are independent), the corresponding equation system has a unique solution.
Show Question
Question 17. (Third-order determinants)
Find the determinant of the matrix
$$A=\begin{bmatrix}8&3&0\\6&4&1\\-2&1&3\end{bmatrix}$$
Q17 Answer
The determinant of the matrix
$$A=\begin{bmatrix}8&3&0\\6&4&1\\-2&1&3\end{bmatrix}$$
Can be calculated as follows:
| \(|A|\) | \(=8\begin{vmatrix}4&1\\1&3\end{vmatrix}+3\color{red}{(-1)}\begin{vmatrix}6&1\\-2&3\end{vmatrix}+0\begin{vmatrix}6&4\\-2&1\end{vmatrix}\) |
| \(=8(12-1)-3(18-(-2))+0\) | |
| \(=88-60=28\) |
Note:
Third-order determinants can be established in terms of the lower-order determinants using a row or a column. This is called the Laplace expansion.
If the Laplace expansion is done using the elements of the first row, then the second element of row one is to be multiplied by \(-1\).
The following pattern of the sign is used for the Laplace expansion of third-order determinants:
$$\begin{bmatrix}+&-&+\\-&+&-\\+&-&+\end{bmatrix}$$
Please see the recommended books.
Show Question
Question 18 (Third-order determinants)
Find the determinant of the following matrices:
$$A=\begin{bmatrix}4&3&0\\1&6&2\\3&1&3\end{bmatrix}$$
$$B=\begin{bmatrix}2&3&1\\3&7&5\\0&0&1\end{bmatrix}$$
$$C=\begin{bmatrix}4&3&5\\1&6&2\\10&18&14\end{bmatrix}$$
Q18 Answer
Given the matrices
$$A=\begin{bmatrix}4&3&0\\1&6&2\\3&1&3\end{bmatrix}$$
$$B=\begin{bmatrix}2&3&1\\3&7&5\\0&0&1\end{bmatrix}$$
$$C=\begin{bmatrix}4&3&5\\1&6&2\\10&18&14\end{bmatrix}$$
$$|A|=73$$
$$|B|=5$$
$$|C|=0$$
Note:
The determinant of an \(n×n\) matrix is
$$|A|=a_{i1} C_{i1}+a_{i2} C_{i2}+⋯+a_{in} C_{in}$$
Where,
• \(a_{ij}\) is the element in row \(i\) and column \(j\)
• \(C_{ij}\) is the cofactor of the element \(a_{ij}\). Next few questions discuss how to find a minor and a cofactor of an element of a matrix.
Above approach is called the Laplace expansion of a matrix to find the determinant. The Laplace expansion can be done using any column also:
$$|A|=a_{1j} C_{1j}+a_{2j} C_{2j}+⋯+a_{nj} C_{nj}$$
Show Question
Question 19. (Third-order determinants)
Use determinants to check whether a unique solution exists for each of the following systems of equations:
(a)
| \(4x+3y+5z\) | \(=21\) |
| \(x+6y+2z\) | \(=15\) |
| \(3x+y\) | \(=0\) |
(b)
| \(4x+3y+3z\) | \(=20\) |
| \(x+2y+4z\) | \(=8\) |
| \(3x+y-z\) | \(=12\) |
Q19 Answer
(a) Given the equation system,
| \(4x+3y+5z\) | \(=21\) |
| \(x+6y+2z\) | \(=15\) |
| \(3x+y\) | \(=0\) |
The coefficient matrix is
$$A=\begin{bmatrix}4&3&5\\1&6&2\\\color{red}{3}&\color{red}{1}&\color{red}{0}\end{bmatrix}$$
Its determinant can be calculated as follows:
| \(|A|\) | \(=\color{red}{3}\begin{vmatrix}3&5\\6&2\end{vmatrix}+\color{red}{1(-1)}\begin{vmatrix}4&5\\1&2\end{vmatrix}+\color{red}{0}\begin{vmatrix}4&3\\1&6\end{vmatrix}\) |
| \(=\color{red}{3}(6-30)-\color{red}{1}(8-5)+0\) | |
| \(=-72-3=-75 ≠0\) |
The coefficient matrix is a nonsingular matrix. All equations, therefore, are independent. A unique solution exists.
See that we performed the Laplace expansion using the third row as the calculation using third row is easier as one of its elements is zero.
(b) Given the system
| \(4x+3y+3z\) | \(=20\) |
| \(x+2y+4z\) | \(=8\) |
| \(3x+y-z\) | \(=12\) |
The coefficient matrix is $$A=\begin{bmatrix}4&3&3\\1&2&4\\3&1&-1\end{bmatrix}$$ The determinant of the coefficient matrix is zero, hence the coefficient matrix is a singular matrix. There exists linear dependence between at least two rows or columns. Hence, in the equation system, all equations are not independent. A unique solution, therefore, does not exist.
Note:
Properties of a determinant are helpful tools to evaluate the determinant. Some of these properties are:
• If a nonzero multiple of one row (or one column) is added with another row (or another column), it will not change the value of the determinant.
• If an element of any row (or column) is multiplied by a constant, all elements of that row (or column) must be multiplied by that constant. If a row or a column is multiplied by a constant, the determinant is also multiplied by that constant.
• If there exists linear dependence between two or more rows or columns, the determinant is zero, no matter if other rows or columns are independent.
For example, in the equation system given at (b) where the coefficient matrix is
$$A=\begin{bmatrix}4&3&3\\1&2&4\\3&1&-1\end{bmatrix}$$
There exists linear dependence among the rows. Here Row 1 = Row 2+ Row 3. Therefore, its determinant is zero.
Read more about the properties of matrix and determinant from Dowling E T, Mathematical Economics.
Show Question
Question 20. (Minors and cofactors)
Find the minors \((|M_{ij}|)\) and cofactors \((|C_{ij}|)\) of the following matrix
$$A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}$$
Q20 Answer
Given the Matrix
$$A=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}$$
The minors are:
$$|M_{11} |=a_{22} |M_{12}|=a_{21}\\|M_{21}|=a_{12} |M_{22} |=a_{11}$$
And the cofactors are:
$$|C_{11}|=(-1)^{1+1} a_{22} |C_{12}|=(-1)^{1+2}a_{21}$$
$$|C_{21} |=(-1)^{2+1} a_{12} |C_{22}|=(-1)^{2+2} a_{11}$$
Cofactors can be simplified as:
$$|C_{11}|=a_{22} |C_{12}|=-a_{21}$$
$$|C_{21}|=-a_{12} |C_{22}|=a_{11}$$
Note:
To find the minor of an element \(a_{ij}\) in matrix \(A\), that is to find \(|M_{ij}|\)
• delete the row \(i\) and column \(j\) of \(A\)
• deleting the row \(i\) and column \(j\) of \(A\), form a sub-matrix with the remaining elements.
• \(|M_{ij}|\) is the determinant of the sub-matrix which is formed after deleting the row \(i\) and column \(j\) of \(A\).
• In this way for each element in \(A\), corresponding minor can be determined.
• For example, in the given matrix, the minor of the element \(a_{11}\) is \(|M_{11}|=a_{22}\) which is obtained by deleting the first row and first column of the matrix.
• The minor of the element \(a_{21}\) is \(|M_{21}|=a_{21}\) which is obtained by deleting the second row and first column of the matrix.
• Similarly, we can find the minor of each element by deleting the corresponding row and column from the matrix and using the remaining elements in the sub-matrix.
A cofactor is a minor with a prescribed sign. To find the cofactor of an element \(a_{ij}\) in matrix \(A\), that is to find \(|C_{ij}|\):
• Find the minor \(|M_{ij}|\)
• Multiply the minor by \((-1)^{i+j}\)
That is,
$$|C_{ij}|=(-1)^{i+j}|M_{ij}|$$
For example, while the minor of \(a_{21}\) is \(|M_{21}|=a_{12}\), the cofactor of \(a_{21}\) is
$$|C_{21}|=(-1)^{2+1} a_{12}=-a_{12}$$
Show Question
Question 21. (Minors and cofactors)
Find the minors \((|M_{ij}|)\) and cofactors \((|C_{ij}|)\) of the following matrix
$$A=\begin{bmatrix}4&3\\1&2\end{bmatrix}$$
Q21 Answer
Given the matrix
$$A=\begin{bmatrix}4&3\\1&2\end{bmatrix}$$
The minors are:
$$|M_{11}|=2 |M_{12}|=1$$
$$|M_{21}|=3 |M_{22}|=4$$
And the cofactors are:
$$|C_{\color{red}{11}}|=(-1)^{\color{red}{1+1}} (2) |C_{\color{red}{12}}|=(-1)^{\color{red}{1+2}}(1)$$
$$|C_{\color{red}{21}}|=(-1)^{\color{red}{2+1}} (3) |C_{\color{red}{22}} |=(-1)^{\color{red}{2+2}} (4)$$
Cofactors can be simplified as:
$$|C_{11}|=2 |C_{12}|=\color{red}{-1}$$
$$|C_{21}|=\color{red}{-3} |C_{22}|=4$$
Show Question
Question 22. (Minors and cofactors)
Find the minors (\(|M_{ij}|\)) and cofactors (\(|C_{ij}|\)) of the following matrix
$$A=\begin{bmatrix}4&3&5\\1&6&2\\3&1&0\end{bmatrix}$$
Q22 Answer
Given the matrix
$$A=\begin{bmatrix}4&3&5\\1&6&2\\3&1&0\end{bmatrix}$$
We get \(9\) minors and \(9\) cofactors.
To start with finding the cofactor of \(a_{11}\), that is to find \(|M_{11}|\), we need to delete the first row and first column and form the sub-matrix

The determinant of this sub-matrix is the corresponding minor \(|M_{11}|=0-2=-2\).
Similarly, we can find all minors:
| \(|M_{11}|\) | \(=-2\) |
| \(|M_{12}|\) | \(=-6\) |
| \(|M_{13}|\) | \(=-17\) |
| \(|M_{21}|\) | \(=-5\) |
| \(|M_{22}|\) | \(=-15\) |
| \(|M_{23}|\) | \(=-5\) |
| \(|M_{31}|\) | \(=-24\) |
| \(|M_{32}|\) | \(=3\) |
| \(|M_{33}|\) | \(=21\) |
We know that a cofactor is a corresponding minor with a prescribed sign, that is, $$|C_{ij}|=(-1)^{i+j} |M_{ij}|$$ Here the cofactors are:
| \(|C_{11}|\) | \(=-2\) |
| \(|C_{12}|\) | \(=\color{red}{6}\) |
| \(|C_{13}|\) | \(=-17\) |
| \(|C_{21}|\) | \(=\color{red}{5}\) |
| \(|C_{22}|\) | \(=-15\) |
| \(|C_{23}|\) | \(=\color{red}{5}\) |
| \(|C_{31}|\) | \(=-24\) |
| \(|C_{32}|\) | \(=\color{red}{-3}\) |
| \(|C_{33}|\) | \(=21\) |
Note:
To get the cofactors from the minors, use the following sign pattern to multiply the minors:
$$\begin{bmatrix}+&\color{red}{-}&+\\\color{red}{-}&+&\color{red}{-}\\+&\color{red}{-}&+\end{bmatrix}$$
Show Question
Question 23. (Inverse Matrix)
Find the inverse matrix of the following matrix
$$A=\begin{bmatrix}4&2\\1&1\end{bmatrix}$$
Q23 Answer
Given the matrix
$$A=\begin{bmatrix}4&2\\1&1\end{bmatrix}$$
Check the singularity:
Its determinant is \(|A|=4-2=2≠0\). The given matrix is a non-singular matrix and the inverse matrix, hence, exists.
Find the cofactors and replace each element of the matrix by the corresponding cofactor to form the cofactor matrix:
$$C=\begin{bmatrix}\color{red}{1}&\color{red}{-1}\\-2&4\end{bmatrix}$$
Transpose the cofactor matrix to get the adjoint matrix of \(A\):
$$A=\begin{bmatrix}\color{red}{1}&-2\\\color{red}{-1}&4\end{bmatrix}$$
Multiply the adjoint matrix by \({{1}\over |A|}\) to get the inverse matrix:
$$A^{-1}={{1}\over 2}×\begin{bmatrix}1&-2\\-1&4\end{bmatrix}$$
$$=\begin{bmatrix}{{1}\over 2}&-{{1}\over 2}\\-{{1}\over 2}&{{4}\over 2}\end{bmatrix}$$
$$=\begin{bmatrix}0.5&-1\\-0.5&2\end{bmatrix}$$
Note:
The inverse matrix of a matrix \(A\) can be found if and only if the matrix is a square, nonsingular matrix. Inverse matrix is generally denoted by \(A^{-1}\), if exists.
If the inverse matrix \(A^{-1}\) exists, it satisfies the relation:
$$AA^{-1}=I=A^{-1} A$$
There are a few approaches available to find the inverse matrix if the given matrix is a square and nonsingular matrix. One frequently used method is:
$$A^{-1}={{1}\over |A|}adj A$$
The steps are:
• Find \(|A|\). If \(|A|≠0\), proceed to the next step.
• Find the cofactor matrix of \(A\) by replacing each element of \(A\) by the corresponding cofactor (see, minors and cofactors).
• Take the transpose matrix of the cofactor matrix which is called the adjoint matrix.
• Multiply the adjoint matrix by \({{1}\over |A|}\) to get the inverse matrix.

Funny example of an inverse matrix (With due respect for two great movies: Matrix and Matrix reloaded.)
Show Question
Question 24. (Inverse Matrix)
Find the inverse matrix of the following matrix
$$A=\begin{bmatrix}4&3\\2&5\end{bmatrix}$$
Q24 Answer
Given the matrix
$$A=\begin{bmatrix}4&3\\2&5\end{bmatrix}$$
Check the singularity:
Its determinant is \(|A|=20-6=14≠0\). The given matrix is a non-singular matrix and the inverse matrix, hence, exists.
Find the cofactors and replace each element of the matrix by the corresponding cofactor to form the cofactor matrix:
$$C=\begin{bmatrix}\color{red}{5}&\color{red}{-2}\\-3&4\end{bmatrix}$$
Transpose the cofactor matrix to get the adjoint matrix of \(A\):
$$adj A=\begin{bmatrix}\color{red}{5}&-3\\\color{red}{-2}&4\end{bmatrix}$$
Multiply the adjoint matrix by \({{1}\over |A|}\) to get the inverse matrix:
$$A^{-1}={{1}\over 14}×\begin{bmatrix}5&-3\\-2&4\end{bmatrix}$$
$$=\begin{bmatrix}{{5}\over 14}&-{{3}\over 14}\\-{{2}\over 14}&{{4}\over 14}\end{bmatrix}$$
Show Question
Question 25. (Inverse Matrix)
Find the inverse matrix of the following matrix
$$A=\begin{bmatrix}4&2&2\\2&3&1\\2&1&0\end{bmatrix}$$
Q25 Answer
Given the Matrix
$$A=\begin{bmatrix}4&2&2\\2&3&1\\2&1&0\end{bmatrix}$$
Check the singularity:
Its determinant is \(|A|=-8≠0\). The given matrix is a non-singular matrix and the inverse matrix, hence, exists.
Find the cofactors and replace each element of the matrix by the corresponding cofactor to form the cofactor matrix: $$C=\begin{bmatrix}-1&2&-4\\2&-4&0\\-4&0&8\end{bmatrix}$$ Transpose the cofactor matrix to get the adjoint matrix of \(A\): $$adj A=\begin{bmatrix}-1&2&-4\\2&-4&0\\-4&0&8\end{bmatrix}$$ Multiply the adjoint matrix by \({{1}\over |A|}\) to get the inverse matrix: $$A^{-1}={{1}\over -8}×\begin{bmatrix}-1&2&-4\\2&-4&0\\-4&0&8\end{bmatrix}$$ $$=\begin{bmatrix}{{1}\over 8}&-{{1}\over 4}&{{1}\over 2}\\-{{1}\over 4}&{{1}\over 2}&0\\{{1}\over 2}&0&-1\end{bmatrix}$$
Note:
Use recommended books to do more practice if you need to use the inverse matrix of a \(3×3\) matrix in any course. It’s not difficult, but it requires practice.
Show Question
Question 26. (Matrix inversion to solve a system of linear equations)
Using matrix inversion solve the following system of linear equations:
$$8x+4y+2z=14\\4x+y-z=12$$
Q26 Answer
Given the system
$$8x+4y+2z=14\\4x+y-z=12$$
Its matrix form is:
$$AX=B$$
$$\begin{bmatrix}8&4&2\\4&1&-1\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}14\\12\end{bmatrix}$$
As the coefficient matrix is not a square matrix, the inverse matrix of the coefficient matrix cannot be determined. Therefore, using the matrix inversion approach, this system cannot be solved.
Note:
If the coefficient matrix is not a square matrix, its inverse matrix cannot be determined. The corresponding system of linear equations cannot be solved using the method of matrix inversion.
Show Question
Question 27. (Matrix inversion to solve a system of linear equations)
Using matrix inversion solve the following system of linear equations:
$$2x+y=10\\x+y=7$$
Q27 Answer
Given the system
$$2x+y=10\\x+y=7$$
Its matrix form is:
$$AX=B$$
$$\begin{bmatrix}2&1\\1&1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}10\\7\end{bmatrix}$$
The determinant of the coefficient matrix is \(|A|=1\)
The coefficient matrix is a non-singular matrix and the inverse matrix, hence, exists.
The inverse matrix is (use the steps as before):
$$A^{-1}=\begin{bmatrix}1&-1\\-1&2\end{bmatrix}$$
To solve a system of linear equations using the matrix inversion approach use the following relationship, if the inverse matrix exists:
$$X=A^{-1}B$$
| \(\begin{bmatrix}x\\y\end{bmatrix}\) | \(=\begin{bmatrix}1&-1\\-1&2\end{bmatrix}\begin{bmatrix}10\\7\end{bmatrix}\) |
| \(=\begin{bmatrix}10+(-7)\\-10+14\end{bmatrix}\) | |
| \(=\begin{bmatrix}3\\4\end{bmatrix}\) | |
| \(\begin{bmatrix}x\\y\end{bmatrix}\) | \(=\begin{bmatrix}3\\4\end{bmatrix}\) |
Note:
The inverse matrix of a coefficient matrix can be used to solve the system of linear equations if the inverse matrix exists. Remember that, the inverse matrix of a coefficient matrix can only be found if and only if both of the following conditions are met:
• The coefficient matrix is a square matrix. That is, the corresponding system of linear equations has the same number of unknowns (variables) and equations.
• The coefficient matrix is a nonsingular matrix, that is, the determinant of the coefficient matrix is non-zero. If the coefficient matrix is a nonsingular matrix, then the equations in the system of linear equations are independent without which a unique solution cannot be obtained.
Given the equation system in matrix form
$$A_{n×n} X_{n×1}=B_{n×1}$$
If the inverse matrix of the coefficient matrix exists, the relation can be written as:
$$X_{n×1}=A^{-1}_{n×n} B_{n×1}$$
See that the inverse matrix, if exists, \(A^{-1}_{n×n}\), and \(B_{n×1}\) are conformable for multiplication and their product matrix has the dimensions \(n×1\).
Suppose the product matrix of \(A^{-1}_{n×n} B_{n×1}=D\)
Then we can write
| \(X_{n×1}\) | \(=A^{-1}_{n×n} B_{n×1}=D_{n×1}\) |
| \(X_{n×1}\) | \(=D_{n×1}\) |
If two matrices are equal, their corresponding elements are equal, which gives us the solution of the system.
Show Question
Question 28. (Matrix inversion to solve a system of linear equations)
Using matrix inversion solve the following system of linear equations:
$$10x-5y=10\\5x+y=19$$
Q28 Answer
Given the system
$$10x-5y=10\\5x+y=19$$
Its matrix form is:
$$AX=B$$
$$\begin{bmatrix}10&-5\\5&1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}10\\19\end{bmatrix}$$
The determinant of the coefficient matrix is \(|A|=35\)
The coefficient matrix is a non-singular matrix and the inverse matrix, hence, exists.
The inverse matrix is (use the steps as before):
$$A^{-1}=\begin{bmatrix}{{1}\over 35}&{{5}\over 35}\\-{{5}\over 35}&{{10}\over 35}\end{bmatrix}$$
As the inverse matrix of the coefficient matrix exists we can present the system as follows:
$$X=A^{-1}B$$
| \(\begin{bmatrix}x\\y\end{bmatrix}\) | \(=\begin{bmatrix}{{1}\over 35}&{{5}\over 35}\\-{{5}\over 35}&{{10}\over 35}\end{bmatrix}\begin{bmatrix}10\\19\end{bmatrix}\) |
| \(=\begin{bmatrix}{{10}\over 35}+{{95}\over 35}\\-{{50}\over 35}+{{190}\over 35}\end{bmatrix}=\begin{bmatrix}3\\4\end{bmatrix}\) | |
| \(\begin{bmatrix}x\\y\end{bmatrix}\) | \(=\begin{bmatrix}3\\4\end{bmatrix}\) |
Show Question
Question 29. (Matrix inversion to solve a system of linear equations)
Using matrix inversion solve the following system of linear equations:
| \(4x+2y+2z\) | \(=8\) |
| \(2x+3y+z\) | \(=4\) |
| \(2x+y\) | \(=2\) |
Q29 Answer
Given the coefficient matrix
$$A=\begin{bmatrix}4&2&2\\2&3&1\\2&1&0\end{bmatrix}$$
Check the singularity:
Its determinant is \(|A|=-8≠0\). The given matrix is a non-singular matrix and the inverse matrix, hence, exists.
Find the cofactors and replace each element of the matrix by its cofactor to form the cofactor matrix:
$$C=\begin{bmatrix}-1&2&-4\\2&-4&0\\-4&0&8\end{bmatrix}$$
Transpose the cofactor matrix to get the adjoint matrix of \(A\):
$$adj A=\begin{bmatrix}-1&2&-4\\2&-4&0\\-4&0&8\end{bmatrix}$$
Multiply the adjoint matrix by \({{1}\over |A|}\) to get the inverse matrix:
$$A^{-1}={{1}\over -8}×\begin{bmatrix}-1&2&-4\\2&-4&0\\-4&0&8\end{bmatrix}$$
$$=\begin{bmatrix}{{1}\over 8}&-{{1}\over 4}&{{1}\over 2}\\-{{1}\over 4}&{{1}\over 2}&0\\{{1}\over 2}&0&-1\end{bmatrix}$$
As the inverse matrix of the coefficient matrix exists we can present the system as follows:
$$X=A^{-1} B$$
| \(\begin{bmatrix}x\\y\\z\end{bmatrix}\) | \(=\begin{bmatrix}{{1}\over 8}&-{{1}\over 4}&{{1}\over 2}\\-{{1}\over 4}&{{1}\over 2}&0\\{{1}\over 2}&0&-1\end{bmatrix}\begin{bmatrix}8\\4\\2\end{bmatrix}\) |
| \(=\begin{bmatrix}1-1+1\\-2+2+0\\4+0-2\end{bmatrix}=\begin{bmatrix}1\\0\\2\end{bmatrix}\) |
Note:
Please practice from the recommended books.
Show Question
Question 30. (Cramer’s rule to solve a system of linear equations)
Using the Cramer’s rule solve the following system of linear equations:
$$4x+2y=20\\x+y=14$$
Q30 Answer
Given the system
$$4x+2y=20\\x+y=14$$
Its matrix form is:
$$AX=B$$
$$\begin{bmatrix}4&2\\1&1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}20\\14\end{bmatrix}$$
Find the determinant of the coefficient matrix: \(|A|=2\).
Replace column \(1\) of the coefficient matrix by the elements in matrix \(B\) and call the new matrix \(A_1\):
$$A=\begin{bmatrix}\color{red}{4}&2\\\color{red}{1}&1\end{bmatrix}$$
$$A_1=\begin{bmatrix}\color{red}{20}&2\\\color{red}{14}&1\end{bmatrix}$$
Find the determinant of \(A_1\):
$$|A_1 |=-8$$
Divide the determinant of \(A_1\) by the determinant of \(A\) to get the value of the first variable \(x\):
$$x={{|A_1|}\over {|A|}} ={{-8}\over 2}=-4$$
Now replace column 2 of the coefficient matrix by the elements in matrix \(B\) and call the new matrix \(A_2\):
$$A=\begin{bmatrix}4&\color{red}{2}\\1&\color{red}{1}\end{bmatrix}$$
$$A_2=\begin{bmatrix}4&\color{red}{20}\\1&\color{red}{14}\end{bmatrix}$$
Find the determinant of \(A_2\):
$$|A_2 |=36$$
Divide the determinant of \(A_2\) by the determinant of \(A\) to get the value of the second variable \(y\):
$$y={{|A_2 |}\over |A|}={{36}\over 2}=18$$
$$x=-4, y=18$$
Note:
Using Cramer’s rule, we can solve a system of linear equations if a unique solution exists. Cramer’s rule to find the value of \(x_i\) is:
$$x_i={{|A_i|}\over |A|}$$
Here,
\(x_i\) is the \(i\)th unknown variable
\(|A|\) is the determinant of the coefficient matrix.
\(|A_i|\) is the determinant of a special matrix formed by replacing the ith column of the coefficient matrix with the column vector of constants.
To apply the Cramer’s rule:
• The coefficient matrix must be a square matrix, and
• The determinant of the coefficient matrix \(|A|≠0\)
These are equivalent to saying that the linear system of equations has an equal number of unknowns and equations and all equations in the system are independent.
Practice Cramer’s rule from the recommended books
Show Question
Question 31. (Cramer’s rule to solve market equilibrium)
Using the Cramer’s rule find the equilibrium price (\(p\)) and quantity (\(q\)):
$$p=100-2q\\p=10+3q$$
Q31 Answer
Given the system
$$p=100-2q\\p=10+3q$$
It can be rearranged as:
$$p+2q=100\\p-3q=10$$
Its matrix form is:
$$AX=B$$
$$\begin{bmatrix}1&2\\1&-3\end{bmatrix}\begin{bmatrix}p\\q\end{bmatrix}=\begin{bmatrix}100\\10\end{bmatrix}$$
The determinant of the coefficient matrix is \(|A|=-5\)
Replace column 1 of the coefficient matrix by the elements in matrix \(B\) and call the new matrix \(A_1\):
$$A=\begin{bmatrix}1&2\\1&-3\end{bmatrix}$$
$$A_1=\begin{bmatrix}100&2\\10&-3\end{bmatrix}$$
Find the determinant of \(A_1\):
$$|A_1 |=-300-20=-320$$
Divide the determinant of \(A_1\) by the determinant of \(A\) to get the equilibrium value of \(p\):
$$p={{|A_1|}\over |A|}={{-320}\over -5}=64$$
Similarly, you can find the equilibrium value of q:
$$q={{|A_2|}\over |A|}={{-90}\over -5}=18$$
Show Question
Question 32. (Cramer’s rule to solve national income models)
Using the Cramer’s rule find the equilibrium level of \(Y\) and \(C\) given that:
$$Y=C+I_0$$
$$C=C_0+bY$$
Where \(Y\) is the national income and \(C\) is the aggregate consumption. Also, \(I_0\) is the aggregate investment which is assumed to be fixed in this example. Autonomous consumption \(C_0\) and the marginal propensity to consume b are other constants.
Q32 Answer
Given the system
$$Y=C+I_0$$
$$C=C_0+bY$$
It can be rearranged as:
$$Y-C=I_0\\-bY+C=C_0$$
Its matrix form is:
$$AX=B$$
$$\begin{bmatrix}1&-1\\-b&1\end{bmatrix}\begin{bmatrix}Y\\C\end{bmatrix}=\begin{bmatrix}I_0\\C_0\end{bmatrix}$$
The determinant of the coefficient matrix is \(|A|=1-b\)
Replace column 1 of the coefficient matrix by the elements in matrix \(B\) and call the new matrix \(A_1\):
$$A=\begin{bmatrix}\color{red}{1}&-1\\\color{red}{-b}&1\end{bmatrix}$$
$$A_1=\begin{bmatrix}\color{red}{I_0}&-1\\\color{red}{C_0}&1\end{bmatrix}$$
Find the determinant of \(A_1\):
$$|A_1 |=I_0+C_0$$
Divide the determinant of \(A_1\) by the determinant of \(A\) to get the equilibrium value of \(Y\):
$$ Y={{|A_1|}\over |A|}={{I_0+C_0}\over {1-b}}$$
Similarly, you can find the equilibrium value of \(C\):
$$C={{|A_2|}\over |A|}={{C_0+bI_0}\over {1-b}}$$
Show Question
Question 33. (Cramer’s rule to solve national income models)
Using the Cramer’s rule find the equilibrium level of \(Y\) and \(C\) given that:
| \(Y\) | \(=C+I\) |
| \(C\) | \(=100+0.8Y\) |
| \(I\) | \(=I_o=50\) |
Where \(Y\) is the national income and \(C\) is the aggregate consumption.
Q33 Answer
Given the system
| \(Y\) | \(=C+I\) |
| \(C\) | \(=100+0.8Y\) |
| \(I\) | \(=I_o=50\) |
It can be rearranged as:
$$Y-C=50 (I=50)$$
$$-0.8Y+C=100$$
Its matrix form is:
$$AX=B$$
$$\begin{bmatrix}1&-1\\-0.8&1\end{bmatrix}\begin{bmatrix}Y\\C\end{bmatrix}=\begin{bmatrix}50\\100\end{bmatrix}$$
The determinant of the coefficient matrix is \(|A|=1-0.8=0.2\)
Replace column 1 of the coefficient matrix by the elements in matrix \(B\) and call the new matrix \(A_1\):
$$A=\begin{bmatrix}\color{red}{1}&-1\\\color{red}{-0.8}&1\end{bmatrix}$$
$$A_1=\begin{bmatrix}\color{red}{50}&-1\\\color{red}{100}&1\end{bmatrix}$$
Find the determinant of \(A_1\):
$$|A_1|=150$$
Divide the determinant of \(A_1\) by the determinant of \(A\) to get the equilibrium value of \(Y\):
$$Y={{|A_1|}\over |A|}={{150}\over 0.2}=750$$
Similarly, you can find the equilibrium value of \(C\):
$$C={{|A_2|}\over |A|}={{140}\over 0.2}=700 $$
Show Question
Question 34. (IS-LM analysis using Cramer’s rule)
Using the Cramer’s rule find the equilibrium level of \(Y\) and \(r\) given that:
$$sY+ar=I^0+G\\mY-hr=M_s-M^0$$
Where the first equation represents the \(IS\) equation and the second equation represents the \(LM\) equation, and
\(Y=\) net national product
\(r=\) interest rate
Except \(Y\) and \(r\), all other symbols in the given system, for example, \(s\) (marginal propensity to save), a (marginal efficiency of capital), \(I^0\) (Autonomous amount of investment), \(G\) (government expenditure), \(m, h, M_s\) and \(M^0\) are parameters.
For details about the \(IS\) and \(LM\) equations, please read a macroeconomics textbook.
Q34 Answer
Given the system
$$sY+ar=I^0+G\\mY-hr=M_s-M^0$$
Its matrix form is:
$$AX=B$$
$$\begin{bmatrix}s&a\\m&-h\end{bmatrix}\begin{bmatrix}Y\\r\end{bmatrix}=\begin{bmatrix}I^0+G\\M_s-M^0\end{bmatrix}$$
The determinant of the coefficient matrix is \(|A|=-sh-am\)
Using the Cramer’s rule, equilibrium \(Y\) is:
$$Y={{|A_1|}\over |A|}={{-h(I^0+G)-a(M_s-M^0)}\over {-sh-am}}$$
And \(r\) is:
$$r={{|A_2|}\over |A|}={{s(M_s-M^0)-m(I^0+G)}\over {-sh-am}}$$
Show Question
Question 35. (IS-LM analysis using Cramer’s rule)
Using the Cramer’s rule find the equilibrium level of \(Y\) and \(r\) given that:
$$0.2Y+100r=180\\0.3Y-150r=240$$
Where
\(Y=\) net national product
\(r=\) interest rate
The first equation is the \(IS\) equation.
The second equation represents the \(LM\) equation.
Q35 Answer
Given the system
$$0.2Y+100r=180\\0.3Y-150r=240$$
Its matrix form is:
$$AX=B$$
$$\begin{bmatrix}0.2&100\\0.3&-150\end{bmatrix}\begin{bmatrix}Y\\r\end{bmatrix}=\begin{bmatrix}180\\240\end{bmatrix}$$
The determinant of the coefficient matrix is \(|A|=-60\)
Using the Cramer’s rule, equilibrium \(Y\)is:
$$Y={{|A_1|}\over |A|}={{-51000}\over {-60}}=850$$
And \(r\) is:
$$r={{|A_2|}\over |A|}={{-6}\over {-60}}=0.1$$
Show Question
Question 36. (MCQ: Matrix and determinant)
Given three matrices
$$A=\begin{bmatrix}2&5&6\\11&8&10\end{bmatrix}$$
$$B=\begin{bmatrix}4&2\\2&3\end{bmatrix}$$
$$C=\begin{bmatrix}2&4\\5&7\\3&10\end{bmatrix}$$
Which of the followings are conformable for multiplication?
a) \(AB\)
b) \(BA\)
c) \(BC\)
d) \(CB\)
e) \(AC\)
Q36 Answer
Given three matrices
$$A=\begin{bmatrix}2&5&6\\11&8&10\end{bmatrix}$$
$$B=\begin{bmatrix}4&2\\2&3\end{bmatrix}$$
$$C=\begin{bmatrix}2&4\\5&7\\3&10\end{bmatrix}$$
Which of the followings are conformable for multiplication?
a) \(AB\)
b) \(BA\)
c) \(BC\)
d) \(CB\)
e) \(AC\)
Answer: \(BA\), \(CB\), and \(AC\) are conformable for multiplication
Show Question
Question 37. (MCQ: Matrix and determinant)
Given three matrices
$$A=\begin{bmatrix}2&5&6\\11&8&10\end{bmatrix}$$
$$B=\begin{bmatrix}4&2\\2&3\end{bmatrix}$$
$$C=\begin{bmatrix}2&4\\5&7\\3&10\end{bmatrix}$$
Which of the followings are true? More than one option may be correct.
a) Dimensions of the product matrix \(AB\) are \(2×2\)
b) Dimensions of the product matrix \(BA\) are \(2×2\)
c) Dimensions of the product matrix \(BA\) are \(2×3\)
d) Dimensions of the product matrix \(CB\) are \(3×2\)
e) Dimensions of the product matrix \(CA\) are \(2×2\)
Q37 Answer
Given three matrices
$$A=\begin{bmatrix}2&5&6\\11&8&10\end{bmatrix}$$
$$B=\begin{bmatrix}4&2\\2&3\end{bmatrix}$$
$$C=\begin{bmatrix}2&4\\5&7\\3&10\end{bmatrix}$$
Which of the followings are true? More than one option may be correct.
a) Dimensions of the product matrix \(AB\) are \(2×2\)
b) Dimensions of the product matrix \(BA\) are \(2×2\)
c) Dimensions of the product matrix \(BA\) are \(2×3\)
d) Dimensions of the product matrix \(CB\) are \(3×2\)
e) Dimensions of the product matrix \(CA\) are \(2×2\)
Answer: Options c and d are correct. Other options are incorrect.
Show Question
Question 38. (MCQ: Matrix and determinant)
Given two matrices
$$A=\begin{bmatrix}2&5&6\\11&8&10\end{bmatrix}$$
$$C=\begin{bmatrix}2&4\\5&7\\3&10\end{bmatrix}$$
Which of the followings is the product matrix \(AC\)?
a) \(AC=\begin{bmatrix}40&60\\80&100\end{bmatrix}\)
b) \(AC=\begin{bmatrix}47&103\\92&200\end{bmatrix}\)
c) \(AC=\begin{bmatrix}200&103\\920&47\end{bmatrix}\)
d) Cannot be determined
Q38 Answer
Given two matrices
$$A=\begin{bmatrix}2&5&6\\11&8&10\end{bmatrix}$$
$$C=\begin{bmatrix}2&4\\5&7\\3&10\end{bmatrix}$$
Which of the followings is the product matrix \(AC\)?
a) \(AC=\begin{bmatrix}40&60\\80&100\end{bmatrix}\)
b) \(AC=\begin{bmatrix}47&103\\92&200\end{bmatrix}\)
c) \(AC=\begin{bmatrix}200&103\\920&47\end{bmatrix}\)
d) Cannot be determined
Answer: b
Show Question
Question 39. (MCQ: Matrix and determinant)
Given a system of linear equation
$$2x+3y=10\\x-2y=6$$
Which of the followings is the matrix form of the given system? More than one options may be correct.
a) \(\begin{bmatrix}2&3\\1&-2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}10\\6\end{bmatrix}\)
b) \(\begin{bmatrix}1&-2\\2&3\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}6\\10\end{bmatrix}\)
c) \(\begin{bmatrix}3&2\\-2&1\end{bmatrix}\begin{bmatrix}y\\x\end{bmatrix}=\begin{bmatrix}10\\6\end{bmatrix}\)
d) \(\begin{bmatrix}-2&1\\3&2\end{bmatrix}\begin{bmatrix}y\\x\end{bmatrix}=\begin{bmatrix}6\\10\end{bmatrix}\)
Q39 Answer
Given a system of linear equation
$$2x+3y=10\\x-2y=6$$
Which of the followings is the matrix form of the given system? More than one options may be correct.
a) \(\begin{bmatrix}2&3\\1&-2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}10\\6\end{bmatrix}\)
b) \(\begin{bmatrix}1&-2\\2&3\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}6\\10\end{bmatrix}\)
c) \(\begin{bmatrix}3&2\\-2&1\end{bmatrix}\begin{bmatrix}y\\x\end{bmatrix}=\begin{bmatrix}10\\6\end{bmatrix}\)
d) \(\begin{bmatrix}-2&1\\3&2\end{bmatrix}\begin{bmatrix}y\\x\end{bmatrix}=\begin{bmatrix}6\\10\end{bmatrix}\)
Answer: All four options are correct.
Show Question
Question 40. (MCQ: Matrix and determinant)
Given four matrices
$$A=\begin{bmatrix}10&12\\5&6\end{bmatrix} B=\begin{bmatrix}4&2\\2&3\end{bmatrix}$$
$$C=\begin{bmatrix}5&2\\10&4\end{bmatrix} D=\begin{bmatrix}5&2\\2&4\end{bmatrix}$$
Which of the matrices are singular? More than one option may be correct.
a) A
b) B
c) C
d) D
e) None of the above
Q40 Answer
Given four matrices
$$A=\begin{bmatrix}10&12\\5&6\end{bmatrix} B=\begin{bmatrix}4&2\\2&3\end{bmatrix}$$
$$C=\begin{bmatrix}5&2\\10&4\end{bmatrix} D=\begin{bmatrix}5&2\\2&4\end{bmatrix}$$
Which of the matrices are singular? More than one option may be correct.
a) A
b) B
c) C
d) D
e) None of the above
Answer: a) A and c) C are singular matrices.
Show Question
Question 41. (MCQ: Matrix and determinant)
Given the matrix
$$A=\begin{bmatrix}9&7&8\\11&5&20\\2&0&0\end{bmatrix}$$
Find the determinant of the matrix.
a) \(100\)
b) \(200\)
c) \(300\)
d) \(400\)
e) None of the above
Q41 Answer
Given the matrix
$$A=\begin{bmatrix}9&7&8\\11&5&20\\2&0&0\end{bmatrix}$$
Find the determinant of the matrix.
a) \(100\)
b) \(200\)
c) \(300\)
d) \(400\)
e) None of the above
Answer: b) \(200\)
Show Question
Question 42. (MCQ: Matrix and determinant)
Given the matrix
$$A=\begin{bmatrix}3&1\\8&2\end{bmatrix}$$
Which one is the inverse matrix?
a) \(A^{-1}=\begin{bmatrix}2&-1\\-8&3\end{bmatrix}\)
b) \(A^{-1}=\begin{bmatrix}1&0.5\\4&1.5\end{bmatrix}\)
c) \(A^{-1}=\begin{bmatrix}-1&0.5\\4&-1.5\end{bmatrix}\)
d) \(A^{-1}=\begin{bmatrix}-1&-0.5\\-4&-1.5\end{bmatrix}\)
Q42 Answer
Given the matrix
$$A=\begin{bmatrix}3&1\\8&2\end{bmatrix}$$
Which one is the inverse matrix?
a) \(A^{-1}=\begin{bmatrix}2&-1\\-8&3\end{bmatrix}\)
b) \(A^{-1}=\begin{bmatrix}1&0.5\\4&1.5\end{bmatrix}\)
c) \(A^{-1}=\begin{bmatrix}-1&0.5\\4&-1.5\end{bmatrix}\)
d) \(A^{-1}=\begin{bmatrix}-1&-0.5\\-4&-1.5\end{bmatrix}\)
Answer: c) \(A^{-1}=\begin{bmatrix}-1&0.5\\4&-1.5\end{bmatrix}\)
Show Question
Question 43. (MCQ: Matrix and determinant)
Given the matrix
$$A=\begin{bmatrix}10&6\\7&4\end{bmatrix}$$
Which of the followings are true? More than one option may be correct.
a) \(|A|=-2\)
b) \(C=\begin{bmatrix}4&-7\\-6&10\end{bmatrix}\)
c) \(Adj A=\begin{bmatrix}4&-6\\-7&10\end{bmatrix}\)
d) \(A^{-1}=\begin{bmatrix}-2&3\\3.5&-5\end{bmatrix}\)
Q43 Answer
Given the matrix
$$A=\begin{bmatrix}10&6\\7&4\end{bmatrix}$$
Which of the followings are true? More than one option may be correct.
a) \(|A|=-2\)
b) \(C=\begin{bmatrix}4&-7\\-6&10\end{bmatrix}\)
c) \(Adj A=\begin{bmatrix}4&-6\\-7&10\end{bmatrix}\)
d) \(A^{-1}=\begin{bmatrix}-2&3\\3.5&-5\end{bmatrix}\)
Answer: All options are correct.
Show Question
Question 44. (MCQ: Matrix and determinant)
Given a system of linear equations
$$2x+6y=20\\-x+5y=-10$$
Suppose the coefficient matrix is \(A\). Suppose \(A_i\) is a special matrix formed by replacing the column \(i\) of the coefficient matrix with the column vector of constants. Which of the followings are true? More than one option may be correct.
a) \( |A|=16\)
b) \( |A_1 |=160\)
c) \( |A_2 |=0\)
d) \(x=10, y=0\)
Q44 Answer
Given a system of linear equations
$$2x+6y=20\\-x+5y=-10$$
Suppose the coefficient matrix is \(A\). Suppose \(A_i\) is a special matrix formed by replacing the column \(i\) of the coefficient matrix with the column vector of constants. Which of the followings are true? More than one option may be correct.
a) \( |A|=16\)
b) \( |A_1 |=160\)
c) \( |A_2 |=0\)
d) \(x=10, y=0\)
Answer: All options are correct.
Show Question
Question 45. (MCQ: Matrix and determinant)
Given a system of linear equations
$$2x+6y+z=35\\-x+5y+2z=21\\3x+y-z=14$$
Which of the followings are true? More than one option may be correct.
a) \(|A|=0\)
b) A unique solution exists
c) A unique solution does not exist
d) There exists a linear dependence in the system.
e) \( x=2, y=5, z=1\)
Q45 Answer
Given a system of linear equations
$$2x+6y+z=35\\-x+5y+2z=21\\3x+y-z=14$$
Which of the followings are true? More than one option may be correct.
a) \(|A|=0\)
b) A unique solution exists
c) A unique solution does not exist
d) There exists a linear dependence in the system.
e) \( x=2, y=5, z=1\)
Answer: Options a, c, and d are correct.
Show Question
Question 46. (MCQ: Matrix and determinant)
Given a system of linear equations
$$2x+4y-3z=24\\3x-5y+2z=26\\-x+3y+2z=34$$
Which of the followings are true? More than one option may be correct.
a) \( |A|=0\)
b) A unique solution exists
c) A unique solution does not exist
d) There exists a linear dependence in the system.
e) \( |A|=-76\)
Q46 Answer
Given a system of linear equations
$$2x+4y-3z=24\\3x-5y+2z=26\\-x+3y+2z=34$$
Which of the followings are true? More than one option may be correct.
a) \( |A|=0\)
b) A unique solution exists
c) A unique solution does not exist
d) There exists a linear dependence in the system.
e) \( |A|=-76\)
Answer: Options b and e are correct.
Show Question
Question 47. (MCQ: Matrix and determinant)
Given a system of linear equations
$$0.4Y+150r=200\\0.1Y-250r=30$$
Which of the following is true if Cramer’s rule is applied?
a) \(|A|=0\)
b) \(|A|=100\)
c) \(|A_1|=-54, 500\)
d) \(|A_2|=-20\)
Q47 Answer
Given a system of linear equations
$$0.4Y+150r=200\\0.1Y-250r=30$$
Which of the following is true if Cramer’s rule is applied?
a) \(|A|=0\)
b) \(|A|=100\)
c) \(|A_1|=-54, 500\)
d) \(|A_2|=-20\)
Answer: Option c is correct.
Show Question
Question 48. (MCQ: Matrix and determinant)
Given a system of linear equations
$$0.4Y+150r=378\\0.1Y-250r=60$$
Which of the followings are correct if Cramer’s rule is applied? More than one option may be correct.
a) \(|A|=0\)
b) \(|A|=-115\)
c) \(|A_1|=-94, 500\)
d) \( Y=900\)
Q48 Answer
Given a system of linear equations
$$0.4Y+150r=378\\0.1Y-250r=60$$
Which of the followings are correct if Cramer’s rule is applied? More than one option may be correct.
a) \(|A|=0\)
b) \(|A|=-115\)
c) \(|A_1|=-94, 500\)
d) \( Y=900\)
Answer: Options b, c, and d are correct.
Show Question
Question 49. (MCQ: Matrix and determinant)
Given a system of linear equations
$$Y-C=50\\-0.8Y+C=100$$
Find the correct options. More than one option may be correct.
a) \(|A|=2\)
b) \(C=\begin{bmatrix}1&0.8\\1&1\end{bmatrix}\)
c) \(Adj A=\begin{bmatrix}1&1\\0.8&1\end{bmatrix}\)
d) \(A^{-1}=\begin{bmatrix}5&5\\4&5\end{bmatrix}\)
e) \( A^{-1} B=\begin{bmatrix}750&700\end{bmatrix}\)
Q49 Answer
Given a system of linear equations
$$Y-C=50\\-0.8Y+C=100$$
Find the correct options. More than one option may be correct.
a) \(|A|=2\)
b) \(C=\begin{bmatrix}1&0.8\\1&1\end{bmatrix}\)
c) \(Adj A=\begin{bmatrix}1&1\\0.8&1\end{bmatrix}\)
d) \(A^{-1}=\begin{bmatrix}5&5\\4&5\end{bmatrix}\)
e) \( A^{-1} B=\begin{bmatrix}750&700\end{bmatrix}\)
Answer: Options b, c, and d are correct. Option e is not correct as it must be a column vector, not a row vector.
Show Question
Question 50. (A funny question about Matrix)
Who was the lead actor in ‘The Matrix’ and ‘Matrix Reloaded’?
a) Keanu Reeves
b) Leonardo DiCaprio
c) Pierce Brosnan
d) Dwayne Johnson
Q50 Answer
Who was the lead actor in ‘The Matrix’ and ‘Matrix Reloaded’?
a) Keanu Reeves
b) Leonardo DiCaprio
c) Pierce Brosnan
d) Dwayne Johnson
Answer: a) Keanu Reeves
Show Question
Recommended Books
Alpha C. Chiang, Fundamental Methods of Mathematical Economics, Fourth Edition, McGraw-Hill, 2006
Carl P. Simon and Lawrence Blume, Mathematics for Economists, WW Norton & Company, 1994
Edward T. Dowling, Introduction to Mathematical Economics, Third Edition, McGraw-Hill, 2001
Geoff Renshaw, Maths for Economics, Fourth Edition, Oxford University Press, 2016
Mike Rosser, Basic Mathematics for Economics, Second Edition, Routledge, 2003
Michael Hoy, John Livernois, Chris McKenna, Ray Rees, and Thanasis Stengos, Mathematics for Economics, PHI Learning Private Limited.
Teresa Bradley, Essential Mathematics for Economics and Business, Fourth Edition, Wiley, 2013
Thank You