Section 1

The slope of non-linear functions

Suppose \(y = f(x)\) is a non-linear function. Also, suppose that we want to measure the slope of the function \(y = f(x)\) at point \(x_{0}\). Graphically, to measure the slope of the function at \(x_{0}\) we need to draw a tangent line to the graph of \(f\) at point \((x_{0}, f(x_{0}))\). If the tangent drawn at \((x_{0}, f(x_{0}))\) is a unique one, the slope of the tangent line is a very good measure of the slope of the function \(y = f(x)\) at the point \((x_{0}, f(x_{0}))\). The slope of the tangent line may be different at different point of a non-linear function.

Figure 1(\(a\)) shows the tangent line to a non-linear function \(y = f(x)\) at a point \(x_{0}\). Figure 1 (\(b\)) shows two tangent lines to the same non-linear function \(y = f(x)\) at two different points.

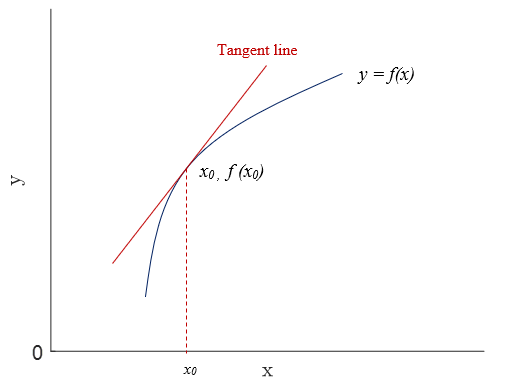
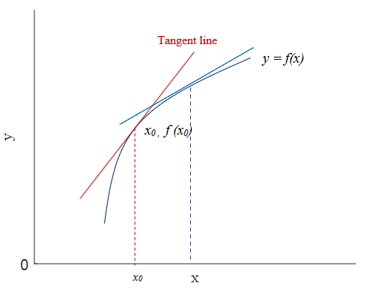
To sum up, the slope of a non-linear function may be different at a different point. The slope of the tangent line at \((x_{0}, f(x_{0}))\) is the slope of the function \(y = f(x)\) at \(x_{0}\).

Derivative: The slope of the tangent line at point \(x_{0}\) is the derivative of the function \(y = f(x)\) at that point:

\({f}'(x_{0}) \qquad \) or \( \qquad \frac{df}{dx}(x_{0})\)